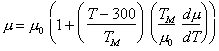CHAPTER 9

---

THE COVALENT ELEMENTS, Si AND Ge

 

9.1 General Features of the Mechanical Behaviour of the Diamond Cubic Elements

9.2 Data for Silicon and Germanium

References for Chapter 9

 

 

FOUR elements crystallize in the diamond cubic structures: silicon, germanium, α-tin and diamond itself. It can be thought of as an f.c.c. structure with two atoms associated with each f.c.c. atom position.  Each atom has four nearest neighbours to which it is linked by four purely covalent bonds. The low co-ordination makes it a very open structure, with a low density.  But despite this, the covalent elements are enormously strong, having a flow strength at which exceeds μ/20 at 0 K and which remains high even at 0.5 T_M. Their mechanical properties are interesting because they typify the extreme behaviour associated with pure covalent bonding.

 

            Maps and data for silicon and germanium are shown in Figs. 9.1 to 9.4.  The parameters used to compute the maps are listed in Table 9.1.

 

TABLE 9.1 The covalent elements

 

           

             The mechanical behaviour of Si and Ge is dominated by their localized, strongly directional, covalent bonding.  It creates an exceptionally large lattice resistance for slip on all slip systems, includ­ing the primary system  (Alexander and Haasen, 1968).  The result is that the normalized flow strength at below half the melting point is larger than that for any other class of solid (except perhaps ice). It is so large that, in most modes of loading, covalent elements and compounds fracture before they flow.  The hardness test allows the plastic behaviour to be studied in a simple way down to 0.2 T_M, when fracture becomes a problem here also.

            The localized nature of the bonding has other consequences: the energy of formation and motion of point defects is large, so that diffusion (at a given homologous temperature) is slower than in other classes of solid.  At high temperature ( > 0.6 T_M) Si and Ge show power- law creep, often complicated by an inverse transient (in creep tests) or a yield drop (in constant strain- rate tests) during which the dislocation density increases towards a steady state.  This steady state is rarely reached in the small strains of most published experiments, although Myshlyaev  et al. (1969) [1] report steady behaviour in silicon.  We have assumed that steady-state creep can be described by the rate-equation used in earlier sections for metals (eqn. (2.21)) and that, at suffici­ently low stresses, diffusional flow (as described by eqn. (2.29)) will appear . Both creep mechanisms are diffusion-controlled, and are slow because of the slow rates of diffusion.  Thus, the covalent elements and the covalently bonded 3-5 and 2-6 compounds, as a class, are stronger (in terms of the normalized variable σ_s/μ) at all homologous temperatures, than any other class of solid; the ultimate example, of course, is diamond.  The maps are a tolerably good fit to the hardness data except below 0.2 T_M (when fracture often occurs round the indenter) and to the high- temperature (>0.8 T_M) creep data.  At inter­mediate temperatures, the maps match the creep data less well.  Lower yield point and transient creep data, some of which are shown on Fig. 9.3, deviate widely from the predicted steady-state behaviour of the maps (as expected) and were ignored in deriving the parameters used in their construction.

            The stress axes of the maps shown in this chapter have been extended upwards by a factor of 10 compared with the others in this book.  This is because, for the reasons already given, the data lie at higher normalized stresses than those for most other materials; and because it allows us to show where certain pressure- induced phase transformations would occur in simple compression (using the pressure   that would appear in a uniaxial compression test).  These phase trans­formations could become important in hardness tests, when the hydrostatic pressure at yield is roughly three times larger for the same equivalent shear stress, σ_s.

            There is extensive literature on the mechanical properties of silicon and germanium. The interested reader should refer to Alexander and Haasen (1968) [2] for a comprehensive review.

 

 

 

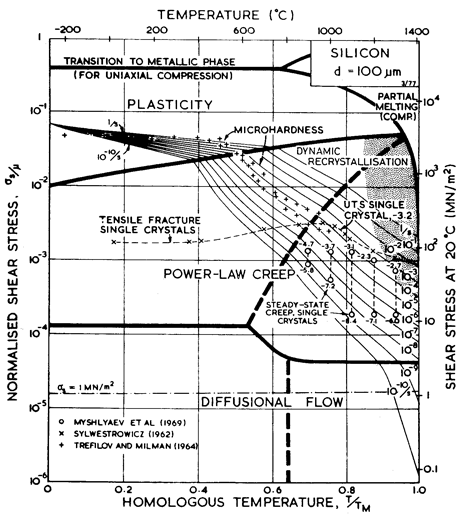
Fig. 9.1. Stress/temperature map for silicon of grain size 100 µm. Data are labelled with log₁₀ ().

 

 

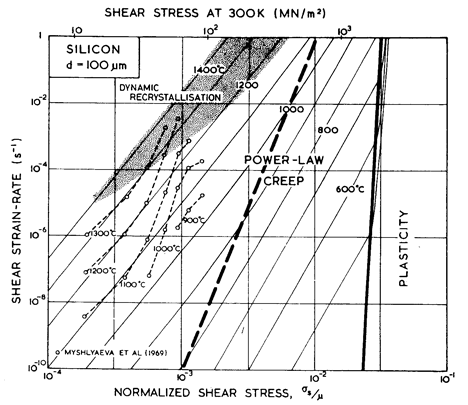
Fig. 9.2. Strain-rate/stress map for silicon of grain size 100 µm. Data are labelled with temperature (°C).

 

 

Fig.9.3. Stress/temperature map for germanium of grain size 100 µm. Data are labelled with log₁₀().

 

 

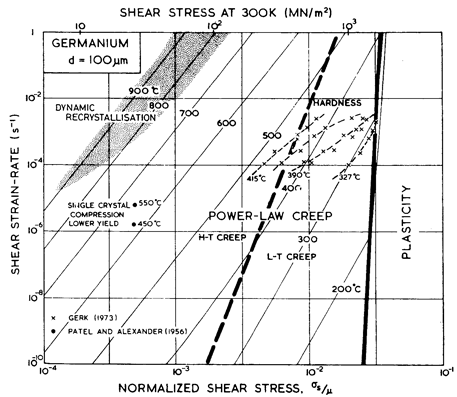
Fig. 9.4. Strain- rate/stress map for germanium of grain size 100 µm. Data are labelled with temperature (°C).

 

 

9.2 DATA FOR SILICON AND GERMANIUM

<Back to Top>

 

            The modulus and its temperature dependence were calculated from single- crystal data using:

and the data of McSkimin (1953, 1959)  [3, 4] and McSkimin and Andreatch (1963, 1964) [5, 6].

            Dislocations and slip systems in diamond cubic crystals have been reviewed by Alexander and Haasen (1968) [2]. Under normal circumstances, slip occurs on , giving the five independent systems necessary for polycrystal plasticity.

            The low-temperature yield strength (T < 0.5 T_M) is based on the micro- hardness measurements of Trefilov and Mil'man (1964) [7] corrected according to Marsh (1964) [8].  In both cases the temperature dependence of the hardness is less than can be explained using realistic values of ∆F_p, and the rate­equation, using the constants of Table 9.1, does not match the measured hardness below 0.2 T_M very well (this may be because fracture occurred at the indenter).

            The power- law creep constants for silicon were fitted to the steady- state single- crystal creep data of Myshlyaev et al (1969) [1]. In the range of their measurements they observed an activation energy of between 400 and 520 kJ/mole; that for self­diffusion is 496 kJ/mole (Masters and Fairfield, 1966) [9] which therefore provides an approximate description of their results.  The use of a power- law, too, is an approximation (Fig. 9.2); our values of n = 5 and A = 2.5 x 10⁶ provide the best fit.

            We have found no steady- state creep data for germanium. Brown et al. (1971) [10], studying transient creep, found an activation energy of around 340 kJ/mole, which is rather larger than that for lattice diffusion of 287 kJ/mole (Letaw  et al., 1956) [11].  Useful information is contained in the high- temperature hardness measurements of Gerk (1975) [12] and Trefilov and Mil'man (1964) [7] which are plotted on Figs. 9.3 and 9.4. Gerk's data suggest a power- law with n = 3; but because the hot- hardness test does not approach steady-state conditions, we have fitted the data to a power- law with the same exponent, n, as that for silicon (namely 5), adjusting the constant A to fit Gerk's data. This choice leads to better agreement with the hardness data of Trefilov and Mil'man (1964) [7] than the alternative choice of n = 3 suggested by Gerk (1975) [12].

 

 

References for Chapter 9

<Back to Top>

 

1.         Myshlyaev, M.M., V.I. Nikitenko, and V.I. Nesterenko, Phys. Stat. Sol., 1969. 36: p. 89.

2.         Alexander, H. and P. Haasen, Dislocations and plastic flow in the diamond structure. Solid State Physics, 1968. 22: p. 27.

3.         McSkimin, H.J., J. Acoust. Soc. Am., 1959. 31: p. 287.

4.         McSkimin, H.J., Measurement of elastic constants at low temperatures by means of ultrasonic waves: data for silicon and germanium single crystals, and for fused silica. Journal of Applied Physics, 1953. 24: p. 988.

5.         McSkimin, H.J. and P.J. Andreatch, Elastic moduli of silicon vs hydrostatic pressure at 25^oC and -195.8^oC. Journal of Applied Physics, 1964. 35: p. 2161-65.

6.         McSkimin, H.J. and P.J. Andreatch, Elastic moduli of germanium versus hydrostatic pressure at 25.0 ^oC and -195.8 ^oC. Journal of Applied Physics, 1963. 34: p. 651-55.

7.         Trefilov, V.I. and Y.V. Mil'man, Soviet Physics Doklady, 1964. 8: p. 1240.

8.         Marsh, D.M. Plastic flow in glass. in Proc. R. Soc. 1964.

9.         Masters, B.J. and J.M. Fairfield, Silicon self-diffusion. Applied Physics Letters, 1966. 8: p. 280.

10.       Brown, D., G. Chaudhari, and P. Feltham, Energy barriers in high-temperature creep of Ge and LiF single crystals. Philosophical Magazine( before 1978), 1971. 24: p. 213-16.

11.       Letaw, H., W.M. Portnoy, and L. Slifkin, Self-diffusion in germanium. Phys. Rev., 1956. 102: p. 636.

12.       Gerk, A.P., Germanium microhardness and the correlation of indentation creep with dislocation. Philosophical Magazine( before 1978), 1975. 32: p. 355-65.