CONSTRUCTION OF THE MAPS
3.2 Superposition of Rate-Equations
SEVEN or more mechanisms, described in Chapter 2, contribute to the deformation of crystalline solids. The one which is dominant (meaning that it contributes most to the total rate of deformation) depends on the stress and temperature to which the solid is exposed, and on its properties. It is helpful, for a given material, to have a way of plotting the field of dominance of each mechanism and of displaying both the experimental data and the predictions that the model-based equations of Section 2 make for it. Such a diagram (or "map") summarizes in a compact form both the experimental and model-based understanding of the materials (Ashby, 1972 [1]; Frost and Ashby, 1973 [2]).
Ways
of doing this were introduced briefly in Chapter 1, and illustrated, for
nickel, by Figs. 1.2 to 1.6. For the reasons given there, it is preferable to
use as axes, the macroscopic variables σs/μ,
T/TM,
![]() , and, when discussing non-steady-state behaviour (Chapter 17, Section 17.1), the strain
γ, or the time t. Of the
possible combinations, we have found that with axes of
σs/μ and T/TM (Fig. 1.2) and that with
axes of
, and, when discussing non-steady-state behaviour (Chapter 17, Section 17.1), the strain
γ, or the time t. Of the
possible combinations, we have found that with axes of
σs/μ and T/TM (Fig. 1.2) and that with
axes of
![]() and
σs/μ (Fig.
1.3) are the most useful: the first covers the full range of all the
macroscopic variables, and best allows comparison of theory and experiment at
low temperatures, while the second displays the creep regime, and permits
accurate comparison of theory and experiment at high temperatures. They appear
throughout Chapters 4 to 16. The map with axes of
and
σs/μ (Fig.
1.3) are the most useful: the first covers the full range of all the
macroscopic variables, and best allows comparison of theory and experiment at
low temperatures, while the second displays the creep regime, and permits
accurate comparison of theory and experiment at high temperatures. They appear
throughout Chapters 4 to 16. The map with axes of
![]() and
T/TM has merit for
displaying behavior at very high strain rates (Chapter 17, Section 17.2).
and
T/TM has merit for
displaying behavior at very high strain rates (Chapter 17, Section 17.2).
A deformation map for a material is constructed by the following procedure. Examples of each step will be found throughout Chapters 4 to 16.
First, data for the material properties are gathered: lattice parameter, molecular volume, and Burger's vector; moduli and their temperature dependencies; and lattice, boundary and core diffusion coefficients (if they exist). It is often necessary to replot data for moduli and diffusion coefficients in order to make a sensible choice of constants, μ0, dμ/dT, D0υ, Qυ, δD0b, Qb, etc.
Second,
data for the hardness, low-temperature yield, and creep are gathered:
flow strength as a function of temperature and strain rate, and creep rate as a
function of temperature and stress. These data are plotted on transparent paper
with the axes used for the maps themselves: log10 (σs/μ) and T/TM,
or log10 (![]() ) and log10
(σs/μ). Each datum is
plotted as a symbol which identifies its source, and is labeled with the value
of the third macroscopic variable: log10 (
) and log10
(σs/μ). Each datum is
plotted as a symbol which identifies its source, and is labeled with the value
of the third macroscopic variable: log10 (![]() ) or T.
) or T.
Third, an
initial estimate is made of the material properties describing glide (∆F,
![]() ,
∆Fp,
,
∆Fp, ![]() p, etc.) and creep (n, A, etc.) by
fitting eqns. (2.9), (2.12) and (2.21) to these data plots. From the plots it
is also possible to make an initial estimate of the stress at which the simple
power-law for creep breaks down, giving α'
of eqn. (2.26).
p, etc.) and creep (n, A, etc.) by
fitting eqns. (2.9), (2.12) and (2.21) to these data plots. From the plots it
is also possible to make an initial estimate of the stress at which the simple
power-law for creep breaks down, giving α'
of eqn. (2.26).
Fourth, the
initial values for the material properties are used to construct a trial map.
This is best done by a simple computer program which steps incrementally
through the range of σs/μ
and T/TM
(or ![]() and σs/μ), evaluating and
summing the rate-equations at each step, and which plots the result in
the forms shown in Figures which appear in Chapter 1.
and σs/μ), evaluating and
summing the rate-equations at each step, and which plots the result in
the forms shown in Figures which appear in Chapter 1.
All the maps
(regardless of the choice of axes) are divided into fields, within each
of which a given mechanism is dominant. The field boundaries are the
loci of points at which two mechanisms contribute equally to the overall
strain-rate, and are computed by equating pairs (or groups) of
rate-equations, and solving for stress as a function of temperature as shown in
Fig. 3.1. Superimposed on this are the contours of constant strain-rate,
obtained by summing the rate-equations in an appropriate way
(discussed below) to give a total strain-rate,
![]() net and plotting the loci
of points for which
net and plotting the loci
of points for which
![]() net has given constant values, as
shown in Fig. 1.2.
net has given constant values, as
shown in Fig. 1.2.
Fifth, the
data plots are laid over the trial maps, allowing the data to be divided into
blocks according to the dominant flow mechanism. It is then possible to make a
detailed comparison between each block of data and the appropriate rate
equation. The material properties are now adjusted to give the best fit between
theory and experimental data. New maps are now computed and the comparison
repeated. Final adjustments are made by constructing maps of the types
described in Chapter 1, plotting the data onto them, and examining both
goodness-of-fit in individual fields and the precision with which
computed and experimental field boundaries coincided. It cannot be emphasized
too strongly that for the final map to have any real value, this detailed
comparison with data over the entire range T, σs and
![]() is essential.
is essential.
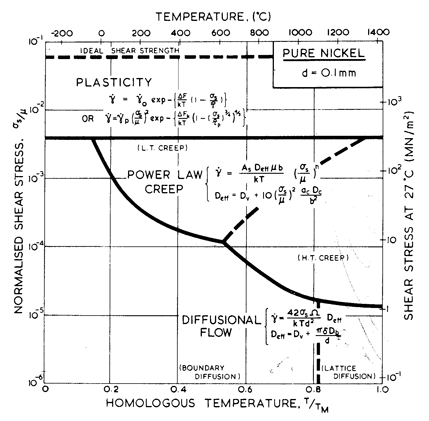
Fig. 3.1. The construction of a deformation-mechanism map. The field boundaries are the loci of points at which two mechanisms (or combinations of mechanisms—see text) have equal rates.
Finally, the adjusted data are tabulated and the maps redrawn, either with data plotted on them, or on separate data-plots. Such tables and plots for each material discussed in this book will be found in Chapters 4 to 16.
The
method of combining the rate-equations requires some discussion. Glide
plasticity is described by two rate-equations (Section 2.2), one for
obstacle-controlled glide (![]() 2, eqn. (2.9)) and one for lattice-resistance-controlled
glide (
2, eqn. (2.9)) and one for lattice-resistance-controlled
glide (![]() 3,
eqn. (2.12)). At the lowest level of approximation, they can be treated as
alternatives:
3,
eqn. (2.12)). At the lowest level of approximation, they can be treated as
alternatives:
|
|
(3.1) |
This is the level adopted here. It is equivalent to assuming that the strongest obstacles control the flow stress, and is entirely adequate for our purposes.
A better approximation is to recognize that, when several strengthening mechanisms (drag, discrete obstacles, lattice resistance) operate at once, their contributions to the flow stress superimpose in a roughly linear way. Even this is an approximation; the superposition is seldom truly linear. The highest precision is possible only by modeling the detailed way in which a given pair of mechanisms interact (see Evans and Rawlings, 1969 [3]; Kocks et al., 1975 [4]; Frost and Ashby, 1971 [5]).
Power-law
creep (![]() 4,
eqn. (2.21) or
4,
eqn. (2.21) or
![]() 6,
eqn. (2.26)) and diffusional flow (
6,
eqn. (2.26)) and diffusional flow (![]() 7, eqn. (2.29)) are independent flow
mechanisms involving different defects. To a first approximation, their strain-rates
add. Powerlaw creep (
7, eqn. (2.29)) are independent flow
mechanisms involving different defects. To a first approximation, their strain-rates
add. Powerlaw creep (![]() 4) and glide (
4) and glide (![]() plas eqn.
(3.1)) do not. Both processes involve the same defect; they describe the same
dislocations moving under different conditions. As the stress is raised, the
gliding part of the motion of a dislocation becomes more important, and the
climbing part less so until, when the boundary between the two fields is reached,
powerlaw climb is not necessary at all. We have solved the problem by treating
power-law creep and glide plasticity as alternative mechanisms, choosing
always the faster one. This divides the map into two parts, one ("power-law
creep") depicting steady-rate flow and one ("plasticity")
depicting flow at constant structure—a consequence of the fact that the glide
equations do not include recovery, and therefore cannot properly describe the
transition from constant-structure to glide-controlled plasticity
at steady state. Harper-Dorn Creep (
plas eqn.
(3.1)) do not. Both processes involve the same defect; they describe the same
dislocations moving under different conditions. As the stress is raised, the
gliding part of the motion of a dislocation becomes more important, and the
climbing part less so until, when the boundary between the two fields is reached,
powerlaw climb is not necessary at all. We have solved the problem by treating
power-law creep and glide plasticity as alternative mechanisms, choosing
always the faster one. This divides the map into two parts, one ("power-law
creep") depicting steady-rate flow and one ("plasticity")
depicting flow at constant structure—a consequence of the fact that the glide
equations do not include recovery, and therefore cannot properly describe the
transition from constant-structure to glide-controlled plasticity
at steady state. Harper-Dorn Creep (![]() 5, eqn. (2.23)) is treated as an
alternative to diffusional flow, again selecting the faster mechanism. Finally,
if the ideal strength is exceeded, flow (
5, eqn. (2.23)) is treated as an
alternative to diffusional flow, again selecting the faster mechanism. Finally,
if the ideal strength is exceeded, flow (![]() l. eqn. (2.1)) becomes catastrophic.
In summary, the net strain rate of a polycrystal subject to a stress as at a
temperature T is:
l. eqn. (2.1)) becomes catastrophic.
In summary, the net strain rate of a polycrystal subject to a stress as at a
temperature T is:
|
|
(3.2) |
Within a
field, the contribution of one mechanism to
![]() net is larger than any other. It
is separated by field boundaries (heavy, full lines) from fields of dominance
of other mechanisms. The power-law creep equation (2.21) and the diffusional flow equation (2.29) each describe the sum of two additive
contributions; heavy broken lines separate the regions of dominance of each
contribution. The contours of constant strain rate are obtained by solving eqn.
(3.2) for as a function of T at constant
net is larger than any other. It
is separated by field boundaries (heavy, full lines) from fields of dominance
of other mechanisms. The power-law creep equation (2.21) and the diffusional flow equation (2.29) each describe the sum of two additive
contributions; heavy broken lines separate the regions of dominance of each
contribution. The contours of constant strain rate are obtained by solving eqn.
(3.2) for as a function of T at constant
![]() net.
net.
The origins and detailed treatment of data are described under the headings of the individual materials. As emphasized earlier, the accuracy of the maps reflects that of the experiments. Different experimenters often report strain-rates that differ by a factor as large as 100 at a given σs and T; it is necessary to judge which experiments more accurately reflect the true material behavior. These judgments are to some extent subjective because of the large number of variables involved: purity, testing atmosphere, grain size, thermomechanical history, recrystallization effects, type of test, and so forth. The effect of impurities is most pronounced in nominally "pure" metals: as little as 0.1% impurity lowers the creep-rate of pure nickel by more than an order of magnitude (Dennison et al., 1966 [6]). The low-temperature yield stress of b.c.c. metals is raised substantially by even smaller amounts of interstitial impurities. Grain size (if not extreme) atmosphere, and test type are less important, but, when relevant, we have tried to record them (grain size appears explicitly on all maps). Dynamic recrystallization can be a problem; it can cause the strain-rate to oscillate (at constant stress) or the flow stress to oscillate (at constant strain-rate) and makes it difficult to define steady-state behavior. If recrystallization (which depends dramatically on purity) occurs only once during a test, it may be neglected in evaluating steady-rate behavior. But if the test produces repeated recrystallization, as is common in hot torsion tests taken to large strains, the successive waves of recrystallization may overlap to produce another type of steady-state behavior. This regime is shown as a shaded region on the maps.
As mentioned
above, the parameters appearing in the rate-equations are adjusted to
give the best description of the experimental data. Most of the adjustment
involves the dislocation creep parameters, n and A and the dislocation glide
parameters
![]() ,
,
![]() and ∆Fp. In some cases the core diffusion coefficients
have been adjusted to fit low-temperature creep data.
and ∆Fp. In some cases the core diffusion coefficients
have been adjusted to fit low-temperature creep data.
The data on which each map is based are plotted on the map or as a separate data plot. Points attached by solid lines have the same strain-rate. A dashed line between points indicates a series of intermediate experimental points. Included on the plots are creep, tension, compression, torsion and (occasionally) extrusion tests, all converted to shear stress. Torsion and extrusion data present difficulties because the stress and strain-rate are not constant throughout the specimen; they must be inferred from a flow-field. The data for single crystals are different: they are plotted as critical resolved shear stress whenever possible, and with the standard conversion from tensile to shear stress (σs = σ/√3) otherwise. To compare them with the polycrystal data shown on the same map, the reader must multiply the single-crystal stresses by the appropriate factor: 1.77 for f.c.c. metals, for instance, and 1.67 for b.c.c. (see Chapter 2, Section 2.2 for further information on Taylor factors). In arriving at the optimized data of the tables shown in later chapters, single-crystal data were treated in this way.
Maps with normalized stress σs/μ and temperature T/TM have, plotted on them, near the bottom, a line of constant shear stress (usually σs = 0.1 MN/m2). This allows the scale on the right-hand edge of the maps (of shear stress at 300 K) to be translated to give the shear stress at any temperature. All maps with T/TM as an axis carry, additionally, a scale of temperature in °C.
1. Ashby, M.F., A first report on deformation-mechanism maps. Acta Metallurgica (pre 1990), 1972. 20: p. 887.
2. Frost, H.J. and M.F. Ashby, A Second Report on Deformation-Mechanism Maps. 1973, Division of Applied Physics, Harvard University.
3. Evans, A.G. and R.D. Rawlings, Thermally activated deformation of crystalline materials. Phys. Stat. Sol., 1969. 34: p. 9-31.
4. Kocks, U.F., A.S. Argon, and M.F. Ashby, Prog. Mat. Sci., 1975. 19: p. 1.
5. Frost, H.J. and M.F. Ashby, Motion of a dislocation acted on by viscous drag on an array of discrete obstacles. J. Appl. Phys, 1971. 42: p. 5273-9.
6. Dennison, J.P., R.J. Llewellyn, and B. Wilshire, The Creep and Fracture Behaviour of Some Dilute Nickel Alloys at 500 and 6000 C. J. Inst. Met., 1966. 94: p. 130-34.