OLIVINES AND SPINELS: Mg2SiO4 AND MgAl2O4
15.1 General Features of the Deformation of Olivines and Spinels
15.2 Data for Forsterite, Mg2SiO4
15.3 Data for Magniesium Aluminate Spinel - MgAl2O4
THE OLIVINES (Mg, Fe)2 SiO4 are orthorhombic. The simplest and most widely studied is forsterite, the magnesium end-member, to which natural olivines are close. It can be thought of as an almost closepacked hexagonal crystal of oxygen (the largest ion) containing silicon and magnesium in some of its tetrahedral and octahedral interstices. The SiO4 tetrahedra are not linked (olivines are not network silicates) so that certain slips are possible without breaking Si—O bonds. For this reason, olivines have somewhat lower creep strengths than network silicates such as SiO2. But examination of the structure shows that general plasticity without diffusion requires slip on additional planes on which Si—O bonds will be broken. Perhaps for this reason, the low temperature strength is high.
The spinels form a second large class of oxides, with the general formula A B2O4. They crystallize in a cubic structure which can be thought of as a combination of the rock-salt and the zinc blende structures. The oxygen ions are close packed in f.c.c. stacking, with the cations contained in the octahedral and tetrahedral interstices.
In the normal spinels, the A2+ ions are contained in the tetrahedral holes, and the B3+ in the octahedral holes: magnesium aluminate spinel, the spinel studied here, is of this type. In the inverse spinels, on the other hand, the A2+ ions and half the B3+ ions are in octahedral holes, and the remaining B3+ ions are in tetrahedral holes. Among the normal aluminate spinels are MgAI2O4, and those obtained on replacing Mg by Fe, Co, Ni, Mn or Zn. Certain ferrites, too, have the normal spinel structure; among them are Zn Fe2O4 and Cd Fe2O4. The inverse spinel structure is adopted by many other ferrites, notably Mg Fe2O4 and those obtained on replacing Mg by Ti, Fe or Ni.
A number of compounds transform from the olivine to the spinel structure on increasing the pressure. Among these are forsterite and the magnesiumrich olivines.
Olivines form the dominant phase in the earth's upper mantle, in which shear must occur when the continental plates move. Much recent work has been motivated by the wish to understand and model this motion (Chapter 19, Section 19.8). Spinels have been studied for different reasons: they are used as refractories and their high strength and transparency makes them attractive for windows which must resist heat, impact or abrasion.
Maps for forsterite and for magnesium aluminate spinel are shown in Figs.15.1 to 15.6. They are based on data plotted on the figures, and the parameters listed in Table 15.1.
TABLE I5.I Olivine and spinel
|
Material |
Mg2SiO4 |
|
MgAl2O4 |
|
|
Crystallographic and thermal data Molecular volume, Ω(m3) Burger's vector, b (m) Melting temperature, TM (K) |
4.92 x 10-29 6.0 x 10-10 2140 |
(a) (b)
|
6.59 x 10-29 5.71 x 10-10 2408 |
(h) (i) (j) |
|
Modulus Shear modulus at 300 K, (MN/m2) Temperature
dependence of modulus, |
8.13 x 104 -0.35 |
(c) (c) |
9.92 x 104 -0.22 |
(k) (k) |
|
Lattice diffusion: oxygen ion Pre-exponential, D0υ (m2/s) Activation energy, Qυ (kJ/mole) |
0.1 522 |
(d) (d) |
8.9 x 10-5 439 |
(1) (1) |
|
Boundary diffusion: oxygen ion Pre-exponential, δD0b(m3/s) Activation energy, Qb (kJ/mole) |
1 x 10-10 350 |
(e) (e) |
1 x 10-14 264 |
(e) (e) |
|
Core diffusion: oxygen ion Pre-exponential, δD0c(m4/s) Activation energy, Qc (kJ/mole) |
— — |
|
3 x 10-25 264 |
(e) (e) |
|
Power-law creep Exponent, n Creep constant, A Activation energy, Qc, (kJ/mole) |
3 0.45 522 |
(f) (f) (f) |
2.7 0.16 — |
(m)
|
|
Obstacle-controlled glide 0
K flow stress, Pre-exponential,
Activation energy, ∆F/μ0b3 |
5 x 10-3 106 0.5 |
|
2 x 10-2 106 0.5 |
|
|
Lattice-resistance-controlled glide O
K flow stress, Pre-exponential,
Activation energy, ∆Fp/μ0b3
|
3.3 x 10-2 1011 0.05 |
(g)
(g) |
8.5 x 10-2 1011 0.033 |
(n)
(n) |
|
(a)The volume of one Mg2SiO4 molecule. (b)See text. (c)Graham and Barsch (1960), and Kamazama and Anderson (1969)
(d)See text and diffusion data plot, Fig. 15.7; Dυ=D0υ exp – (Qυ/RT). (e) No data available. Obtained by taking δD0b=10-9 D0υ and Qb = 0.67 Qυ; δDb= δD0b exp –(Qb/RT), acDc=acD0c exp –(Qc/RT). (f) Fitted to the creep data shown on Fig.15.1. See
Ashby and (1964) Verrall (1977). The value of A is for tensile creep; the
maps computed using.
|
(g) Based principally on hardness data of Evans, cited by Durham and Goetze (1977). (h) The volume of one MgAl2O4 molecule. Crystallographic data from Clark (1966). (i) Mitchell et al. (1976). (j) Handbook of Chemistry and Physics (1972). (k) Calculated from the single-crystal constant Lewis (1966);
(1) Ando and Oishi (1974) for intrinsic oxygen diffusion in MgAl2O4. (m) Fitted to data of Palmour (1966); see also note (f). (n) Fitted to data of Westbrook (1966), using the Marsh correction.
|
|
15.1 GENERAL FEATURES OF THE DEFORMATION OF OLIVINES AND SPINELS |
The mechanical behaviour of both classes of oxide closely resemble that of α-alumina (Chapter 14). This is not surprising since their structures are closely related. All show a high lattice resistance, approaching roughly μ/20 at 0 K, and all retain their strength to high homologous temperatures (0.5 TM and above). Diffusion rates in the spinels and olivines vary somewhat with composition, but are generally comparable with those in Al203. The ratecontrolling species is often assumed to be oxygen, since this is the biggest ion in the structure. But evidence that diffusion of the metal ion can sometimes limit the creep rate in Al2O3 and Fe2O3 (Chapter 14) suggest that similar complications may arise in spinels and olivines also.
The shear modulus and its temperature dependence for olivines have been measured by Graham and Barsch (1969) [1] and Kamazama and Anderson (1969) [2].
The slip systems have been determined by electron microscopy (Phakey et al., 1972 [3]) and optical examination (Raleigh, 1968 [4]; Carter and Ave' Lallemant, 1970 [5]; Young, 1969 [6]; Raleigh and Kirby, 1970 [7]). The easy slip system at low temperatures is that involving dislocations with b = 5.98 [001] Å gliding on (l00) planes. If this slip system is suppressed by proper orientation of the crystal, then dislocations with Burger's vector b=4.76 [100] Å gliding on (010) planes appear. At 1000°C these two systems operate with equal ease. Dislocations with a large Burger's vector (b=10.21 [010] Å on (100)) appear above 800°C, particularly in crystals oriented so that the easy slip system is unstressed. We have used b = 6 x 10-10 m (Table 15.1) since this is broadly typical of the observations.
Data for oxygen transport in olivine are shown in Fig 15.7. Borchardt and Schmaltzried (1972) [8] reported that the oxygen-ion diffusivity at 1320°C was less than 10-17 m2/s; Goetz and Kohlstedt (1973) [9] inferred diffusion coefficients from the kinetics of the annealing of prismatic dislocation loops; and Barnard (1975) [10] measured oxygen ion diffusion by a proton activation method.
Studies of power-law creep in olivine, discussed below, are best described by an activation energy of Qcr = 522 kJ/mol. If we assume that this creep is diffusion controlled, then Qcr can be identified (after minor corrections for the temperature dependence of the modulus) with the activation energy for mass transport in olivine—a process which is probably limited in its rate by oxygen-ion diffusion. We have, therefore, fitted a line with this slope to the data (full line on the figure) for which D0 = 0.1 m2/s and Qυ = 522 kJ/mole. Also shown are plots of the diffusion equation proposed by Goetze and Kohlstedt (1973) [9] (dash-dot line), and that by Stocker and Ashby (1973) [11] (broken line). At high temperature they are all very close, and even at low temperatures the differences are small when compared with scatter in creep and other data.
This diffusion equation
predicts a melting point diffusivity for O2- of 2 x 10-14 m2/s,
compared to an average of around 10-14 m2/s for a
number of other oxides, which, like olivine, have a closepacked oxygen
sublattice, and in which oxygen is thought to diffuse as a single ion. Because
the two numbers are similar we believe oxygen diffuses as a single ion, not as
an ![]() complex.
The grain boundary diffusion coefficients are estimates, using Qb
= 0.6 Qυ and D0b = 2b D0υ.
complex.
The grain boundary diffusion coefficients are estimates, using Qb
= 0.6 Qυ and D0b = 2b D0υ.
Published creep data (Fig. 15.1) for natural and synthetic olivines span the temperature range from 1000 to 1650°C (0.6–0.9 TM) at strain-rates from 10-8 to 10-4/s, often under a confining pressure of up to 103 MN/m2. The results are complicated by the fact that talc was sometimes used as a pressure medium: above 800°C it releases water, which accelerates the creep of these (and most other) silicates. Other experiments avoided these problems by using dry gas to apply pressure when it was required. We have given extra weight to these results in constructing the maps.
All investigators (Carter and Ave' Lallemant, 1970 [5]; Raleigh and Kirby, 1970 [7]; Goetze and Brace, 1972 [12]; Post and Griggs, 1973 [13]; Kirby and Raleigh, 1973 [14]; Kohlstedt and Goetze, 1974 [15]; Durham and Goetze, 1977 [16]; Durham et al., 1977 [17]) report creep rates which are consistent with a value of n which increases from 3 at low stresses to 5 or more at high, with an activation energy of 522 kJ/mol. When all the data for dry olivine are normalized to 1400°C, using an activation energy of 522 kJ/mol, it shows power-law behaviour, with n ≈ 3 at low stresses, followed by a long transition as stress is raised and glide contributes increasingly to the flow (Ashby and Verrall, 1977) [18]. The parameters of Table 15.1 were fitted to these data.
Three studies give information about lowtemperature plasticity in olivines. First, the yield stress for a peridotite (60-70% olivine and 20-30% enstatite) of grain size 0.5 mm, was measured by Carter and Ave' Lallemant (1970) [5] between 325 and 740°C. Secondly, Phakey et al. (1972) [3] obtained stress-strain curves at 600 and 800°C for singlecrystal forsterite. Four compression tests at 800°C with different orientations of the single crystals produced yield stresses ranging from 570 to 1300 MN/m2. The highest value was obtained on the specimen orientated to produce no stress on the easy slip system; we have used this because it is the most representative of a polycrystalline material. Finally, hardness data for olivine exist (Evans, cited by Durham and Goetze, 1977 [16]), and it is this which gives the most complete picture of the low-temperature strength. It and the yield strengths are plotted on Fig. 15.1.

Fig. 15.1. A stress/temperature map for magnesium olivine
with a grain size of 1 mm. Data are labelled with log10(![]() ).
).
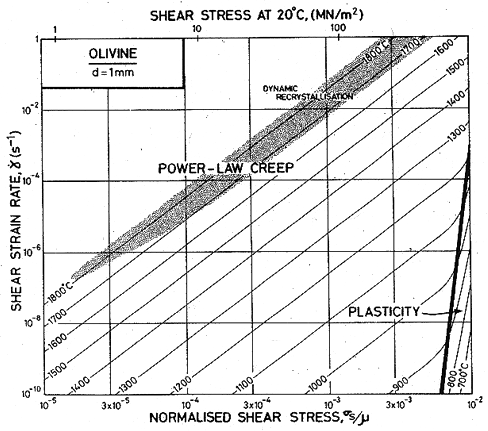
Fig.15.2. A strain-rate/stress map for magnesium olivine with a grain size of 1 mm. Data are shown on Fig. 15.1.
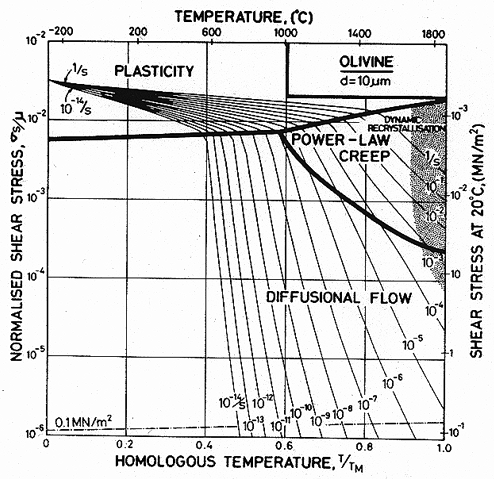
Fig. 15.3. A stress/temperature map for magnesium olivine with a grain size of 10 µm. Data are shown on Fig. 15.1.
The modulus and its temperature dependence were calculated from the single-crystal constant of Lewis (1966) [19] using:
|
|
Magnesium spinel, MgAl2O4, is cubic with a lattice parameter of 8.08 Å. The unit cell contains eight molecules, so that the molecular volume listed in Table 15.1 is one-eighth of the cell volume. Slip has been studied by Mitchell et al. (1976) [20] who found easy slip with a Burger's vector a/2 <110>, which dissociated into a/4 <110> partials. The value listed for b is that for undissociated dislocations.
Oxygen is the slowest-diffusing species in spinel (Oishi and Ando, 1975) [21]. The coefficients measured by Ando and Oishi (1974) [22] and Oishi and Ando (1975) [21] are in fair agreement with those inferred from sintering studies by Bratton (1969, 1971) [23, 24]. We have used the coefficient given by Ando and Oishi for intrinsic oxygen diffusion in MgAl2O4.
The most extensive studies of creep of spinel are those of Palmour and his co-workers. The maps show data from the compression tests of Choi (1965) [25] (see Choi and Palmour, 1965 [26]) and from the bend tests of Palmour (1966) [27]. This second set of tests gave data which lie at stresses which are too low, either because a steady state was not reached, or because of surface cracking. The parameters given in Table 15.1 are fitted to the compression data, and ignore the bend tests.
Diffusion flow was calculated by using the Ando and Oishi (1974) [22] diffusion coefficient for intrinsic lattice diffusion of oxygen, with an effective molecular volume of:
|
Ωeff = Ω/4 |
because there are four oxygen atoms per molecule. Enhanced boundary diffusion has been detected in spinels (Oishi and Ando, 1975) [21] but it is not possible to extract a reliable coefficient from their results. The coefficients listed in Table 15.1 for both boundary and core diffusion are estimates.
The low-temperature strength of spinel is characterized by the hardness measurements of Westbrook (1966) [28]. There is evidence that cracking may have occurred during the test, making some of the data unreliable. The parameters in Table 15.1 are based on the higher hardnesses given by Westbrook, and have been corrected for elastic distortion using the Marsh (1964) [29] correction. The results are then in general agreement with those for Al2O3 (Chapter 14) and BeAl2O4.
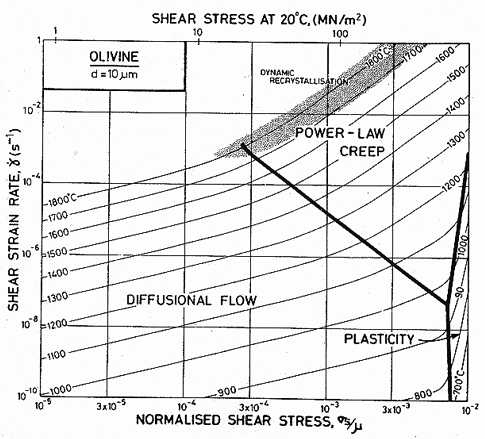
Fig. 15.4. A strain-rate/stress map for magnesium olivine with a grain size of 10 µm. Data are shown on Fig. 15.1.
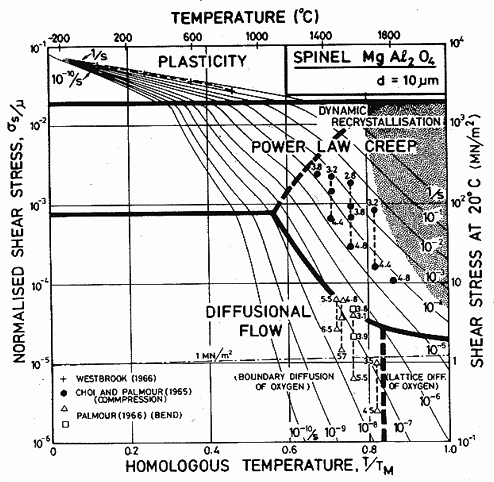
Fig. 15.5. A stress/temperature map for magnesium aluminate
spinel with a grain size of 10
µm. Data are labelled with log10(![]() ).
).

Fig.15.6. A strain-rate/temperature map for magnesium aluminate spinel with a grain size of 10 µm. Data are labelled with the temperature in °C.
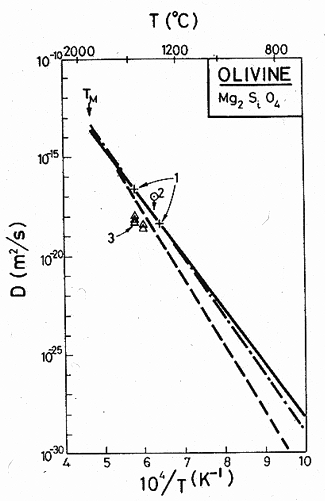
Fig.15.7. Diffusion data for magnesium olivine. The data are from (1) Goetze and Kohlstedt (1973) [9]; (2) Borchardt and Schmatzried (1972) [8]; (3) Barnard (1975) [10].
1. Graham, E.K. and G.R. Barsch, Elastic constants of single crystal forsterite as a function of temperature and pressure. Journal of Geophysical Research, 1969. 64: p. 5949-60.
2. Kamazama, M. and O.L. Anderson, J. Geophys. Res., 1969. 74: p. 5961.
3. Phakey, P., G. Dollinger, and J. Christie. 1972? report, Am. Geophys. Un.
4. Raleigh, C.B., Mechanism of deformation of olivine. J. Geophys. Res., 1968. 73: p. 5391-406.
5. Carter, N.L. and H.G. Ave' Lallemant, Bull. Geol. Soc. Am., 1970. 81.
6. Young, C., Am. J. Sci., 1969. 267: p. 841.
7. Raleigh, C.B. and S.H. Kirby. 1970? Report, Mineral. Soc. Am.
8. Borchardt, G. and H. Schmaltzried, Diffusion in orthosilicates. Ber. Dtsch. Keram. Ges., 1972. 49: p. 5-9.
9. Goetze, C. and D.L. Kohlstedt, Laboratory study of dislocation climb and diffusion in olivine. Journal of Geophysical Research, 1973. 78: p. 5961-71.
10. Barnard, R.S. 1975, Case-Western Reserve University, Department of Materials Science.
11. Stocker, R.L. and M.F. Ashby, On the empirical constants in the Dorn equation. Scripta Met., 1973. 7: p. 115-20.
12. Goetze, C. and W.F. Brace, Tectonophysics, 1972. 113: p. 583.
13. Post, R.L. and D.T. Griggs, The earth's mantle: evidence of non-Newtonian flow, in Science, N.Y. 1973. p. 1242-4.
14. Kirby, S.H. and C.B. Raleigh, Journal of Geophysical Research, 1973. 78: p. 5961.
15. Kohlstedt, D.L. and C. Goetze, Low-stress high-temperature creep in olivine single crystals. Journal of Geophysical Research, 1974. 79: p. 2045-51.
16. Durham, W.B. and C. Goetze, Plastic flow of oriented single crystals of olivine-I. Mechanical data. Journal of Geophysical Research, 1977. 36: p. 5737-53.
17. Durham, W.B., C. Goetze, and B. Blake, Plastic flow of oriented single crystals of olivine-II. Observations and interpretations of the dislocation structures. Journal of Geophysical Research, 1977. 36: p. 5755-70.
18. Ashby, M.F. and R.A. Verrall, Micromechanisms of flow and fracture and their relevance to the rheology of the upper mantle. Phil. Trans. R. Soc. Lond., 1978. A288: p. 59-95.
19. Lewis, M.F., J. Acoust. Soc. Am, 1966. 40: p. 728.
20. Mitchell, T.E., L. Hwang, and A.H. Heuer, Deformation in spinel. Journal of Materials Science, 1976. 11(264): p. 264-72.
21. Oishi, Y. and K. Ando, Self-diffusion of oxygen in polycrystalline MgAl2O3. J. Chem. Phys., 1975. 63: p. 376-8.
22. Ando, K. and Y. Oishi, Self-diffusion coefficients of oxygen ion in single crystals of MgO.nAl2O3 spinels. Journal of Chemical Physics, 1974. 61: p. 625-9.
23. Bratton, R.J., Defect structure of Y2O3-ZrO2 solid solution. Journal of American Ceramic Society, 1969. 52: p. 213-14.
24. Bratton, R.J., Sintering and grain-growth kinetics of MgAl2O4. Journal of American Ceramic Society, 1971. 54: p. 141-143.
25. Choi, D.M. 1965, North Carolina State University at Raleigh (see Choi and Palmour, 1965).
26. Choi, D.M. and H. Palmour, III, Technical Report No. 2. 1965, Army Research Office, Durham, USA.
27. Palmour, H.I. in Proc. Br. Ceram. Soc. 1966.
28. Westbrook, J.H., Rev. Hautes Temper. et Refract., 1966. 3: p. 47.
29. Marsh, D.M. Plastic flow in glass. in Proc. R. Soc. 1964.
