OXIDES WITH THE α-ALUMINA STRUCTURE:
Al2O3, Cr2O3 AND Fe2O3
14.1 General Features of the Mechanical Behaviour of α-Alumina Structured Oxides
14.2 Data for Al2O3
14.3 Data for Cr2O3
14.4 Data for Fe2O3
Three common oxides have the α-alumina structure: corundum or sapphire (Al2O3), chromium sesquioxide (Cr2O3) and hematite (Fe2O3). The structure, if described by its smallest unit cell, is rhombohedral; but it is convenient to think of it in terms of a larger hexagonal unit cell. The oxygen ions are packed in a close-packed hexagonal arrangement with metal ions in two-thirds of the octahedral sites. The unoccupied octahedral sites are ordered within each close-packed layer, and alternate between layers, repeating every third layer. The hexagonal unit cell contains six oxygen layers.
These oxides are generally harder and more refractory than the rock-salt structured oxides, retaining their strength to higher temperatures. Alumina is used as a structural ceramic, as well as an abrasive and a coating for cutting tools. Chromium sesquioxide is perhaps most important as a surface layer on stainless steels and nickel-based alloys.
Maps for the three oxides are shown in Figs. 14.1 to 14.8. The parameters used to construct them are listed in Table 14.1.
TABLE 14.1 Oxides with tbe a-alumina structure
|
Material |
Al203 |
|
Cr203 |
|
Fe203 |
|
|
Crystallographic and thermal data Atomic volume, Ω(m3) Burger's vector, b (m) Melting temperature, TM (K) |
4.25 x 10-29 4.76 x 10-10 2320 |
4.81 x 10-29 4.96 x 10-10 2710 |
(h) (h) |
5.03 x 10-29 5.03 x 10-29 1840 |
(o) |
|
|
Modulus Shear modulus at 300 K, μ0(MN/m2) Temperature
dependence of modulus, |
1.55 x 105
–0.35 |
(a)
(a) |
1.30 x 105
–0.33 |
(i)
(j) |
8.82 x 104
-0.2 |
(p)
(q) |
|
Lattice diffusion: oxygen ion Pre-exponential, D0υ (m2/s) Activation energy, Qυ (kJ/mole) |
0.19 636 |
(b) (b) |
1.59 x 10-3 423 |
(k) (k) |
2.04 x 10-4 326 |
(r) (r) |
|
Lattice diffusion: metal ion Pre-exponential, δD0υ(m2/s) Activation energy, Qυ (kJ/mole) |
2.8 x 10-3 477 |
(c) (c) |
— — |
40 469 |
(s) (s) |
|
|
Boundary diffusion: oxygen ion Pre-exponential, δD0b (m3/s) Activation energy, Qb (kJ/mole) |
10-8 380 |
(d) (d) |
10-15 240 |
(l) (l) |
4 x 10-13 210 |
(t) (u) |
|
Boundary diffusion: metal ion Pre-exponential, δD0b (m3/s) Activation energy, Qb (kJ/mole) |
8.6 x 10-10 419 |
(e) (e) |
— — |
— — |
||
|
Core diffusion Pre-exponential, acD0c (m4/s) Activation energy, Qc (kJ/mole) |
10-22 380 |
(d) (d) |
10-25 240 |
(l) (l) |
2.0 x 10-25 210 |
(l) (l) |
|
Power-law creep Exponent, n Dorn constant, A Activation energy, Qcr (kJ/mole) |
3.0 3.38 — |
(f) (f) |
4.0 1 x 103 — |
(m) (m) |
3.5 5.0 — |
(v) (v) |
|
Obstacle-controlled glide O K flow stress, Pre-exponential, Activation energy, ∆F/μ0b3 |
5 x 10-3 106 0.5 |
5 x 10-3 106 0.5 |
5 x 10-3 106 0.5 |
|||
|
Lattice-resistance; controlled-glide O K flow stress, Pre-exponential, Activation energy, ∆Fp/μ0b3 |
0.05 1011 0.032 |
(g) (g) (g) |
0.05 1011 0.032 |
(n)
(n) |
0.05 1011 0.032 |
(n)
(n) |
|
(a) Tem (1966); (b) Oishi and Kingery (1960), intrinsic oxygen diffusion, see text; Dυ = D0υ exp –(Qυ/RT). (c) Paladino and Kingery (1962). (d) Estimated using Qb=Qc=0.6Qυ (intrinsic); δDb=δD0b exp – (Qb/RT); acDc=acD0c exp – (Qc/RT). (e) Estimate by Cannon and Coble (1974). (f) Based on data of Cannon (1971), high stress
data at 1650°C assuming Qcr, to be that for intrinsic
oxygen diffusion. The value of A is for tensile creep; the
maps are computed using (g) To match the hardness data of Westbrook (1966). |
(h) Based on a = 4.96 A and c = 13.58 A. (i) Rossi and Lawrence (1970); polycrystal data. (j) Yevtushchenko and Levitin (1961); polycrystal data; see note (a). (k) Hagd (1965). (1) Estimated; see note (d). (m) Burton (1975), see note (f). (n) Assumed to be the same as Al2O3. (o) See text. (p) Chou and Sha (1971) see note (a). (q) Anderson et al. (1968j; polycrystal data; see note (a). (r) Hagel (1966). (s) Lindner et al. (1952) as corrected by Hagel (1966). (t) To match creep data as described in text. (u) Channing and Graham (1972). Channing and Graham (1972). (v) Crouch (1972); see note (f). Crouch (1971); see Crouch (1972); see note (f). |
14.1 GENERAL FEATURES OF THE MECHANICAL BEHAVIOUR OF α-ALUMINA STRUCTURED OXIDES |
These oxides are generally stronger than those with the rock-salt structure. By comparing maps for α-alumina (Figs. 14.1-14.4) with those for magnesia (Figs. 12.1-12.4), one sees that the lattice-resistance persists to a much higher temperature (0.5 TM instead of 0.3 TM) and that creep, at the same values of σs/μ and T/TM, is nearly ten times slower. Part of this difference is caused by the structure of α-alumina, which imposes restrictions on slip which do not exist in a simple hexagonal close-packing of ions. Because of the ordered filling of the octahedral sites (described above) certain shears create stacking faults; among these are the simple basal shear and simple twinning, both of which are made much more difficult. The easy slip systems are still those in the basal plane (with slip in the harder prismatic and pyramidal systems appearing at high temperatures) but the overall strength is greater than that of the simpler oxides.
Neither α-alumina nor chromium sesquioxide show any appreciable deviations from exact stoichiometry. Both exist in other allotropic forms, stabilized by temperature and pressure, but no data exist for these and we shall ignore them. Hematite, by contrast, is stable over a range of composition (depending on oxygen partial pressure) and decomposes to Fe3O4 and oxygen before it melts.
Certain problems exist in applying the simple rate equations of Chapter 2 to these oxides. First, there is the problem of relating single crystal to polycrystal behaviour. Both at low temperatures and in creep, polycrystal plasticity is possible only if four or five independent slip systems operate: basal slip alone is insufficient. The polycrystal flow strength reflects some weighted average of the strengths of these systems, and is generally closer to that for the hard system (Hutchinson, 1977) [1]. Where necessary, we have assumed the two to be equal. Similarly, the hardness is taken to be 3√3 times the shear strength of the hard system.
The second problem is that of averaging diffusion coefficients of the components, discussed in Section 12.1 for rock-salt structured oxides. Mass transport requires the motion of metal and oxygen in the ratio 2:3. We therefore form the effective diffusion coefficient:
|
|
and use this in place of the lattice diffusion coefficient. In diffusional flow there is a further problem in picking an appropriate molecular volume Ω. When oxygen is the slower moving species, it is proper to use:
|
Ωeff = Ω/3 |
where Ω is the volume associated with the Al2O3 molecule (since work σΩ/3 done every time one oxygen atom arrives at a surface). When the metal ion is slower, the proper effective volume becomes:
|
Ωeff = Ω/2 |
But diffusion may be extrinsic or intrinsic, and alternative diffusion paths (lattice and grainboundary paths, for instance) may be available. As a general rule the creep rate is determined by the fastest path of the slowest species, and this may change with temperature and grain size as illustrated in Fig. 14.10, which helps understand the disposition of the fields in Figs. 14.3 and 14.4. A further discussion of this point is given in Section 12.1.
The maps have been constructed using these principles. It must be emphasized that the data are very limited. The maps are no better than the data used to construct them, and must be used with caution.
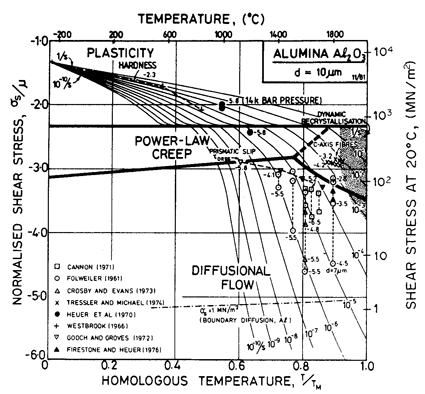
Fig. 14.1. A
stress/temperature map for Al2O3 with a grain size of 10 µm. Data are labelled with log10 (![]() ).
).

Fig. 14.2. A strain-rate/stress map for Al203 with a grain size of 10 µm. Data are labelled with the temperature in °C. Data for larger grain sizes are shown on Fig. 14.4.
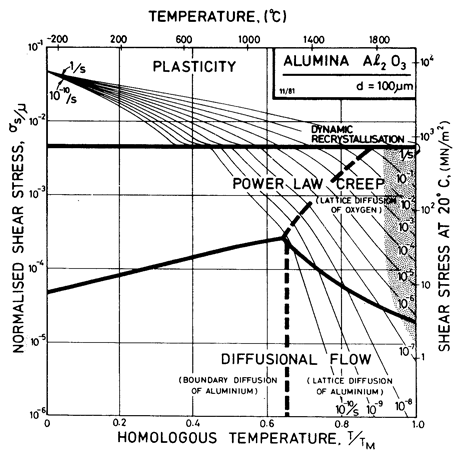
Fig. 14.3. A stress/temperature map for Al2O3 with a grain size of 100 µm. Data are shown on Fig. 14.1.
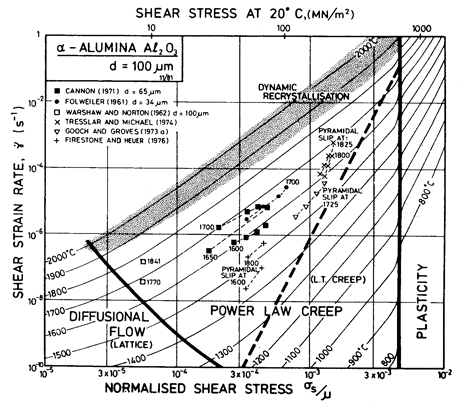
Fig. 14.4. A strain-rate/stress map for Al2O3 with a grain size of 100 µm. Data are labelled with the temperature in °C.
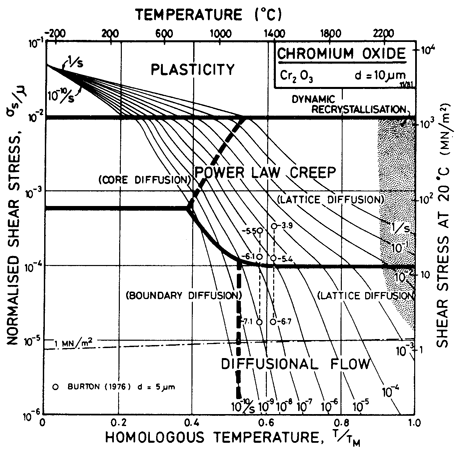
Fig. 14.5. A
stress/temperature map for Cr2O3 with a grain size of 10
µm. Data are labelled with log10 (![]() ).
).

Fig. 14.6. A strain rate/stress map for Cr2O3 with a grain size of 10 µm. Data are labelled with the oxygen partial pressure in MN/m2, the grain size in mm and the temperature in °C.

Fig. 14.7. A
stress/temperature map for Fe203 with a grain size of
10 µm. Data are labelled with log10 (![]() ).
).
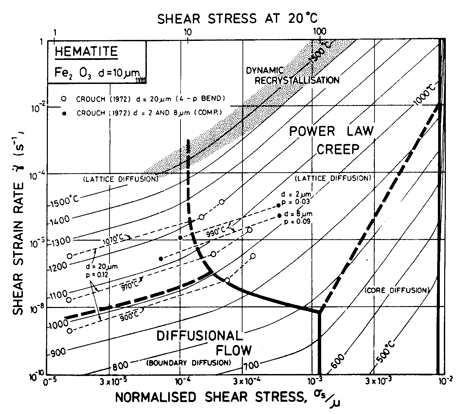
Fig. 14.8. A strain-rate/stress map for Fe2O3 with a grain size of 10 µm. Data are labelled with the temperature in °C.
The modulus μ0 was calculated from:
|
|
using single-crystal data and
their temperature dependence (Tefft, 1966) [2]. This modulus is the one determining the energy of a
![]() screw
dislocation in a trigonal crystal (Chou and Sha, 1971) [3].
screw
dislocation in a trigonal crystal (Chou and Sha, 1971) [3].
Slip and twinning in alumina are discussed by Kronberg (1957) [4]. Because of the complicated packing of aluminium ions, the Burger's vector is large: 2.73 times larger than the oxygen ion spacing. Slip is easiest on the basal plane, but is observed (and required, for polycrystal plasticity) on the prism and pyramidal planes also.
Diffusion data for Al2O3 are shown in Fig. 14.9. Alumina does not deviate significantly from stoichiometry, but small levels of impurity can influence diffusion rates greatly. Cannon and Coble (1974) [5], who have studied and reviewed creep of Al2O3, conclude that its diffusional flow can be understood if the boundary diffusion of oxygen is faster than that of aluminium either in the lattice or in the boundaries. If this is so, a regime will exist in which Al-diffusion controls the creep rate (see Fig. 14.10 and compare Figs. 14.1 and 14.2); data exist which support this view.
For the intrinsic lattice diffusion of oxygen, we have used the data of Oishi and Kingery (1960) [6], shown in the diffusion plot of Fig. 14.9. Lattice diffusion of Al3+ appears to be extrinsic in all available creep experiments (Cannon and Coble, 1974 [5]) . Its rate then depends on the concentration and nature of the impurities. We have used the data of Paladino and Kingery (1962) [7], but when it limits the creep rate, the maps may be unreliable.
For boundary diffusion of Al3+ we have used the estimate of Cannon and Coble (1974) [5], though it leads to a value of Qb/RTM which is exceptionally large. For boundary diffusion of oxygen we have estimated a value in line with data for other oxides. Its value is not critical since it is never ratecontrolling. The core diffusion of oxygen is based on an estimate.
Power-law creep in Al2O3 is much slower than in the rock-salt-structured oxides at the same fraction of the melting point. The maps are based on the compression data of Cannon (1971) [8] for largegrained (65 µm) material, taking a creep exponent n of 3. Cannon reported an activation energy of 611 kJ/mole, large enough to be intrinsic lattice diffusion of oxygen (Table 14.1). These data are generally consistent with measurements of the critical resolved shear stress for pyramidal and for prismatic slip in single crystals.
The lattice-resistance controlled glide parameters are based on the hardness data of Westbrook (1966) [9]. The value of ∆Fp/μ0b3 of 0.032 appears low only because the Burger's vector b is large.
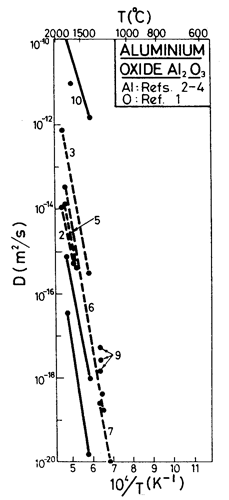
Fig. 14.9. Diffusion data for Al2O3. The data are from: (1) Oishi and Kingery (1960) [6]; (2) Paladino and Kingery (1962) [7]; (3) Folweiler (1961) [10]; (4) Roberts and Roberts (1967) [11]; (5) Warshaw and Norton (1962) [12]; (6) Vishnevskii et al. (1971) [13]; (7) Beauchamp et al. (1961) [14]; (8) Coble and Kingery (1956) [15]; (9) Stavrolakis and Norton (1950) [16]; (10) Jones et al. (1969) .
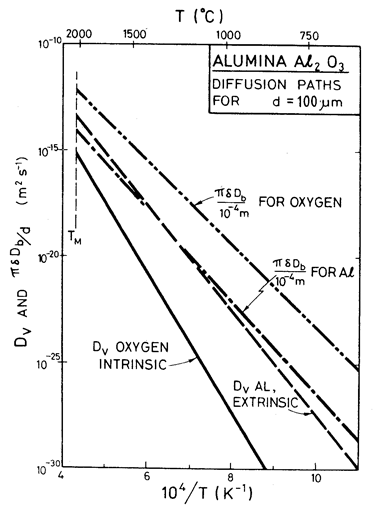
Fig. 14.10. Selected diffusion coefficients for Al2O3 with d = 100 µm, illustrating the selection of the slowest species diffusing by the fastest path.
Modulus measurements for Cr2O3 are confused by the antiferromagnetic to paramagnetic transition at 311 K, at which the shear modulus increases. No single-crystal constants are available, so we have used the polycrystal shear modulus of Rossi and Lawrence (1970) [17] extrapolated to full density, and estimated a temperature dependence from the polycrystal data of Yevtushchenko and Levitin (1961) [18]. Chromium sesquioxide, like alumina, exists only close to stoichiometry. Its slip systems have not been studied and are assumed to be the same as those of alumina.
Lattice diffusion of
oxygen is at least 100 times slower than that of chromium in Cr203
(Fig. 14.11), and should control the rate of creep. We have found no data for
boundary or core diffusion for either species, and have made estimates based on
data for other oxides. Because of the unequal number of Cr3+ and O2–
ions in a molecule, an effective diffusion coefficient ![]() and Qeff =Q/3
must be used in the diffusional flow equation, assuming that oxygen is always
the slower-moving species.
and Qeff =Q/3
must be used in the diffusional flow equation, assuming that oxygen is always
the slower-moving species.
The only creep data for Cr2O3 are those of Burton (1975) [19] shown in Figs. 14.5 and 14.6. They are compatible with power-law behaviour at higher stresses, and with the transition to diffusional flow controlled by oxygen diffusion at lower stresses. There is an indication that a threshold stress may be involved in the diffusional flow field (not shown on the map).
We have found no hardness data for Cr2O3, and have therefore used glide parameters that give the same normalized plastic behaviour as Al2O3 at low temperatures.
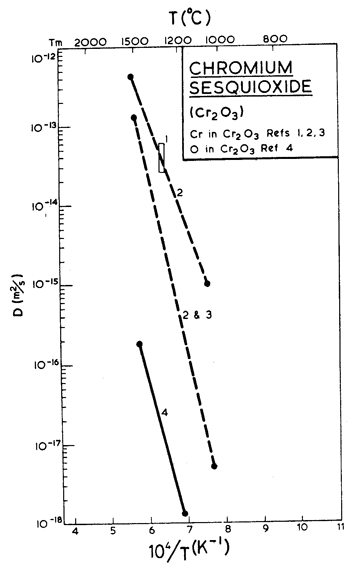
Fig. 14.11. Diffusion data for Cr2O3. The data are from (1) Walters and Grace (1965) [20]; (2) Hagel and Seybolt (1961) [21]; (3) Lindner and Åkerström (1956) [22]; (4) Hagel (1965) [23].
The modulus
μ0 was calculated from the expression for the energy of
a ![]() screw
dislocation in the basal plane of a trigonal crystal:
screw
dislocation in the basal plane of a trigonal crystal:
|
|
given by Chou and Sha (1971) [3], and using the singlecrystal constants cited by them. The temperature dependence is from the polycrystal measurements of Anderson et al. (1968) [24].
The range of stability of Fe2O3 increases with oxygen partial pressure. In air it decomposes to Fe3O4 and O2 at 1663 K; under one atmosphere of oxygen it is stable to 1732 K; and under 16 atmospheres of oxygen, Phillips and Mann (1960) [25] found a eutectic between Fe3O4 and Fe2O3 at 1839 K. The Handbook of Physics and Chemistry (1972) [26] gives the melting point as 1840 K. We have used this value.
Slip systems in Fe2O3 have not been studied. We assume them to be the same as Al2O3.
Lattice diffusion of both Fe3+ and O2-in Fe2O3 have been measured (Fig. 14.12). They are of roughly equal magnitude, requiring the use of an effective diffusion coefficient:
|
|
and, for diffusional flow, an
effective molecular volume Qeff = Q/2.5. At high temperatures Fe2O3
can drift off stoichiometry, changing its diffusion coefficients. Chang and
Wagner (1972) [27], for example, found that the diffusion of iron
decreased with increasing PO2 (they found ![]() ) and Crouch (1972) [28] observed a similar trend in the creep rate (he found
) and Crouch (1972) [28] observed a similar trend in the creep rate (he found ![]() ), although a quantitative explanation
is lacking. We have used the lattice diffusion parameters of Hagel (1966) [29] for oxygen and those of Lindner et al. (1952) [30] for iron. The result is a switch from control by
oxygen diffusion to control by iron diffusion at 1100°C. It is shown as a dashdot
line on Fig. 14.7.
), although a quantitative explanation
is lacking. We have used the lattice diffusion parameters of Hagel (1966) [29] for oxygen and those of Lindner et al. (1952) [30] for iron. The result is a switch from control by
oxygen diffusion to control by iron diffusion at 1100°C. It is shown as a dashdot
line on Fig. 14.7.
We have derived creep
parameters from the data of Crouch (1972) [28] who observed power-law behaviour at higher
stresses and linear behaviour at lower stresses (Figs. 14.7 and 14.8). A
correction is required to compensate for the large porosity (12%) in these
samples. Crouch (1972) [28] reported that ![]() exp 14 φ, where φ is the porosity, so that specimens
of zero porosity should creep more slowly, by a factor of 5, than the data
plotted on Figs. 14.7 and 14.8. This has been taken into account in computing
the maps.
exp 14 φ, where φ is the porosity, so that specimens
of zero porosity should creep more slowly, by a factor of 5, than the data
plotted on Figs. 14.7 and 14.8. This has been taken into account in computing
the maps.
Crouch (1972) [28] interpreted his data in terms of Nabarro Herring creep. But Hay et al. (1973) [31], studying the low-stress creep of Fe2O3 found a grain size dependence which lay between d-2 and d-3, and a creep rate that appears to be too rapid for Nabarro-Herring creep, suggesting control by grain-boundary diffusion. Accordingly, we have calculated boundary diffusion coefficients from these data, and find that the value of δDb shows general agreement with those derived from sintering experiments by Johnson (1973) [32]; and that the activation energy is close to that for the oxidation of Fe3O4 to Fe2O3 (210 kJ/mole; Channing and Graham, 1972 [33]) which is believed to occur by boundary diffusion of oxygen. We have used this activation energy, and a pre-exponential which best matches Crouch's compression tests on fine-grained, lowporosity samples. This is why the fit to the rest of Crouch's data, which had a larger porosity, is poor.
We have found no hardness data for Fe2O3, and have therefore used for low-temperature plasticity the same normalized parameters as for alumina.
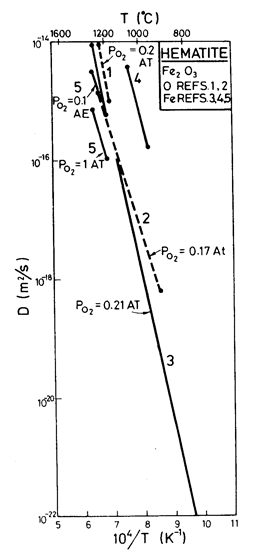
Fig. 14.12. Diffusion data for Fe2O3. The data are from (1) Kingery et al. (1960) [34]; (2) Hagel (1966) [29]; (3) Lindner et al. (1952) [30]; (4) Izvekov et al. (1962) [35]; (5) Chang and Wagner (1972) [27].
1. Hutchinson, J.W., Creep and plasticity of hexagonal polycrystals as related to single crystal slip. Met. Trans., 1977. 8A: p. 1465.
2. Tefft, W.E., J. Res. Natl. Bur. Std., 1966. 70A: p. 277.
3. Chou, Y.T. and G.T. Sha, Dislocation energies in anistropic trigonal crystals. Phys. Stat. Sol. A, 1971. 6(2): p. 505-13.
4. Kronberg, M.L., Plastic deformation of single crystals of sapphire basal slip and twinning. Acta Metallurgica (pre 1990), 1957. 5: p. 507.
5. Cannon, R.M. and R.L. Coble, In "Deformation of Ceramic Materials", in Deformation of Ceramic Materials, R.C.a.T. Bradt, R. E., Editor. 1974, Plenum, NY. p. 61.
6. Oishi, Y. and W.D. Kingery, J. Chem. Phys., 1960. 33: p. 480.
7. Paladino, A.E. and W.D. Kingery, J. Chem. Phys., 1962. 37: p. 957.
8. Cannon, R.M. 1971, Stanford.
9. Westbrook, J.H., Rev. Hautes Temper. et Refract., 1966. 3: p. 47.
10. Folweiler, R.C., Creep behaviour of pore-free polycrystalline aluminium oxide. Journal of Applied Physics, 1961. 32: p. 773-778.
11. Roberts, E.W. and J.P. Roberts, Bull. Soc. Fr. Ceram., 1967. 77: p. 3.
12. Warshaw, S.I. and F.H. Norton, Deformation behaviour of polycrystalline alumina oxide. Journal of American Ceramic Society, 1962. 45: p. 479-486.
13. Vishnevskii, I.I., A.E. I., and N.D. Talyanskaya, Diffusion creep of corundum. Fiz. Tverd. Tela., 1971. 13: p. 3446-9.
14. Beauchamp, E.K., G.S. Baker, and P. Gibbs, WADD Rept. 1961.
15. Coble, R.L. and W.D. Kingery, Effect of porosity on physical properties of sintered alumina. Journal of American Ceramic Society, 1956. 39: p. 377-85.
16. Stavrolakis, J.A. and F.H. Norton, Measurement of the torsion properties of alumina and zirconia at elevated temperatures. J. Am. Ceram. Soc., 1950. 33: p. 263-73.
17. Rossi, L.R. and W.G. Lawrence, Elastic properties of oxide solid solutions: System Al2O3-Cr2O3. J. Am. Ceram. Soc., 1970. 53: p. 604-8.
18. Yevtushchenko, L.A. and R.Z. Levitin, Fiz. Metal. Metalloved, 1961. 12: p. 155.
19. Burton, B., Private communication. 1975.
20. Walters, I.C. and R.E. Grace, Self diffusion of 15Cr in single crystals of Cr2O3. Journal of Applied Physics, 1965. 36: p. 2331-32.
21. Hagel, W.C. and A.U. Seybolt, J. Electrochem. Soc., 1961. 108: p. 1146.
22. Lindner, R. and A. Akerstrom, Z. Phys. Chem. N.F., 1956. 6: p. 162.
23. Hagel, W.C., Anion diffusion of a-Cr2O3. Journal of American Ceramic Society, 1965. 48: p. 70-75.
24. Anderson, O.L., et al., Some elastic constant data on minerals relevant to geophysics. Rev. Geophysics, 1968. 6: p. 491-529.
25. Phillips, B. and A. Mann, J. Phys. Chem., 1960. 64: p. 1452.
26. Handbook of Physics and Chemistry. 54 ed. 1973?check title shown 2 ways chap 10, Cleveland, Ohio, 44128: Chemical Rubber Co., 18901, Cranwood Parkway,.
27. Chang, R.H. and J.B.J. Wagner, Direct-current conductivity and iron tracer diffusion in hematite at high temperatures. Journal of American Ceramic Society, 1972. 55: p. 211-13.
28. Crouch, A.G., High-temperature deformation of polycrystalline Fe2O3. Journal of American Ceramic Society, 1972. 55: p. 558-63.
29. Hagel, W.C., Oxygen-ion diffusion in hematite. Trans. AIME, 1966. 236: p. 179.
30. Lindner, R., S. Anstrurndal, and A. Akerstrom, Acta Chem. Scand., 1952. 6: p. 468.
31. Hay, K.A., A.G. Crouch, and R.T. Pascoe. in International Conference on Physical Metallurgy of Reactor Fuel Elements. 1973.
32. Johnson, D.L., quoted by Hay et al. 1973. 1973?
33. Channing, D.A. and M.J. Graham, A study of iron oxidation processes by Mossbauer spectroscopy. Corrosion Sci., 1972. 12: p. 271-89.
34. Kingery, W.D., D.C. Hill, and R.P. Nelson, Oxygen mobility in polycrystalline NiCr2O3 and a-Fe2O3. Journal of American Ceramic Society, 1960. 43: p. 473-76.
35. Izvekov, V.I., N.S. Gobunov, and A.A. Babad-Zakhrapin, Fiz. Met. Metall., 1962. 14: p. 195.
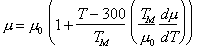 .
.