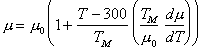OXIDES WITH THE FLUORITE STRUCTURE: UO2 AND ThO2
13.1 General Features of the Deformation of Fluorite-Structured Oxides
Both uranium dioxide and thorium dioxide crystallize with the fluorite (CaF2) structure. They differ from most other oxides in that the metal ion is larger than the oxygen ion and, partly for this reason, diffuses more slowly. Both oxides can be thought of as an f.c.c. stacking of metal ions, with oxygen ions contained in the tetrahedral holes. The oxides PuO2 and CeO2 are like UO2 and ThO2 in the size and packing of their ions. Their mechanical behaviour should closely resemble that described below.
All these oxides exist over a range of composition. They are usually hyperstoichiometric with the composition UO2+x and ThO2+x. Throughout we have tried to select data for oxides close to stoichiometry.
Data and maps for the two oxides are shown in Figs. 13.1 to 13.4. The parameters used to construct them are listed in Table 13.1.
TABLE 13.1 Oxides with the fluorite structure
|
Material |
UO2.00 |
|
ThO2.00 |
|
|
|
Crysrallographic and thermal data Atomic volume, Ω(m3) Burger's vector, b (m) Melting temperature, TM (K) |
4.09 x 10-29 3.87 x 10-10 3080 |
(a) (a) (b) |
4.39 x 10-29 3.96 x 10-10 3520 |
(a) (a) (b) |
|
|
Modulus Shear modulus at 300 K, μ0 (MN/m2) Temperature dependence of modulus, |
9.39 x 104 -0.35 |
(c) (d) |
1.02 x 105 -0.48 |
(k) (l) |
|
|
Lattice diffusion Pre-exponential, D0υ (m2/s) Activation energy, Qυ (kJ/mole) |
1.2 x 10-5 452 |
(e)
|
3.5 x 10-5 625 |
(m) |
|
|
Boundary diffusion Pre-exponential, δD0b (m3/s) Activation energy, Qb (kJ/mole) |
2 x 10-15 293 |
(f) |
10-14 375 |
(n) (n) |
|
|
Core diffusion Pre-exponential, acD0c (m4/s) Activation energy, Qc (kJ/mole) |
10-25 293 |
(g)
|
10-25 375 |
(g) |
|
|
Power-law creep Exponent, n Dorn constant, A |
4.0 3.88 x 103 |
(h) |
4.0 5.2 x 106 |
(o) |
|
|
Obstacle-controlled glide 0 K flow stress, Pre-exponential, Activation energy, ∆Fp/μ0b3 |
3 x 10-3 106 0.5 |
(i)
|
3 x 10-3 106 0.5 |
(p)
|
|
|
Lattice-resistance-controlled-glide 0 K flow stress, Pre-exponential, Activation energy, ∆Fp/μ0b3 |
2 x 10-2 1011 0.08 |
(j)
|
2 x 10-2 1011 0.08 |
(q)
|
|
|
(a) (b) Shunk (1969). (c) Wachtman et al. (1965); (d) Marlowe and Kaznoff (1976).
(e) Diffusion of uranium ions; see also the diffusion plot for UO2, Fig. 13.5. These parameters correspond to the measurements of McNamara (1963). They were chosen because they lie centrally through the data shown in the diffusion plot; Dυ=D0υ exp–(Qυ/RT). (f) Diffusion of uranium ions; Alcock et al. (1966); δDb = δD0b exp –(Qc/RT). (g)A dubious estimate, based on the data for Db; acDc = acD0c exp–(Qc/RT). (h) Based on data of Poteat and Yust (1968). These parameters |
give an exact fit at 1535°C; see Fig 13.2.
The value of A is for tensile creep; the maps were computed
using (i,j) Data are sparse. These parameters give a tolerable fit to the measurements of Radford and Terwilliger (1975) and of Rice (1971). (k) Bechmann and Hearmon (1969); see also note (c). (l) Spinner et al. (1963); see also note (d). (m) Diffusion of thorium ions; see also the diffusion plot for ThO2, Fig. 13.6. These parameters correspond to the measurements of King (1971). They were chosen because the activation energy is close to that for power law creep. (n) Diffusion of thorium ions. The parameters match the data of King (1968) and the activation energy matches certain creep-data —see text. (o) Based on data of Wolfe and Kaufman (1967), see Fig. 13.4; see also note (h). (p,q) Based on data of Ryshkewitch (1941, 1942). Based on data of Ryshkewitch (1941, 1942).
|
||||
13.1 GENERAL FEATURES OF THE DEFORMATION OF FLUORITESTRUCTURED OXIDES |
At low temperatures the fluorite-structured oxides show a substantial lattice resistance, which dominates the mechanical strength up to about 0.4 TM. Hardness studies and compression tests both indicate a flow strength at 0 K of about μ/50.
Above 0.4 TM, the oxides creep. Data for UO2 and ThO2 are detailed on the maps shown as Figs. 13.1 to 13.4. At the higher stresses and larger grain sizes, both oxides exhibit power-law creep, with a creep exponent of about 4. Even though the metal ion is the slower diffusing species, the creep rate depends on the oxygen partial-pressure in the surrounding atmosphere. Seltzer et al. (1971) [1] who have reviewed the creep data for this class of oxides, report that the creep rate of UO2+x increases, and its apparent activation energy decreases, with increasing amounts of excess oxygen (x) probably because it stabilizes vacancies on the uranium sublattice, enhancing uranium-ion diffusion. They found a maximum activation energy of 561 kJ/mole at the composition UO2.00.
At lower stresses the oxides show a well-defined regime of diffusional flow, sometimes with a threshold stress. The creep is almost linear-viscous (n ≈ 1), and strongly dependent on grain size. The maps show that it is well described by the rate equation for diffusional flow (eqn. (2.29)).
Data for UO2 are more extensive than for ThO2 though there is a lack of good hardness measurements for both. Inspection of the maps for UO2 shows that they give a good description of most of the data in all three fields. That for ThO2 is less satisfactory. But the coincidence between the two is good enough that one can conclude with confidence that, when normalized, the mechanical behaviour of the two are closely similar. For this reason we think that oxides with the fluorite structure, in which the cation is larger than the anion, probably form a mechanically-similar class, and that PuO2 and the rare-earth oxides typified by CeO2 probably behave very much as UO2 does.
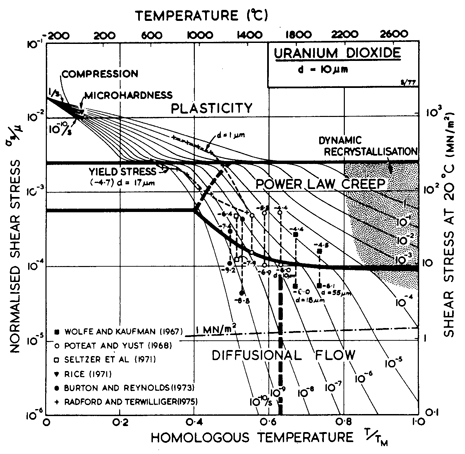
Fig. 13.1. A
stress/temperature map for UO2.00 with a grain size of 10
µm. Data are labelled with log10(![]() ).
).
Fig. 13.2. A strain-rate/stress map-for UO2.00 with a grain size of 10 µm. Data are labelled with the temperature in °C.

Fig. 13.3. A
stress/temperature map for ThO2.00 with a grain size of 10
µm. Data are labelled with log10(![]() ).
).

Fig. 13.4. A strain-rate/stress map for ThO2.00 with a grain size of 10 µm. Data are labelled with the temperature in °C.
The preferred data for the two oxides are listed in Table 13.1. The shear modulus was calculated from single-crystal data (referenced in the table) using:
|
|
Its temperature dependence was obtained from polycrystal data.
The melting
points of these oxides depend on stoichiometry. The values used here are from
Shunk (1969) [2] and refer to
UO2.00 and ThO2.00. Both slip with a slip vector of a ![]() on {100}, {110}
and {111} planes (Edington and Klein, 1966 [3]; Gilbert,
1965 [4]).
on {100}, {110}
and {111} planes (Edington and Klein, 1966 [3]; Gilbert,
1965 [4]).
The diffusion data for the two oxides are shown in Figs. 13.5 and 13.6. The metal (broken line) is the slower-diffusing ion in this class of oxide, and therefore the one likely to control creep and diffusional flow (see Chapter 12, MgO, for a detailed discussion of this point). Although there is considerable spread in quoted activation energies for metal ion diffusion, the figures show that the absolute values are in fairly good agreement. (Measurements of diffusion of oxygen show much greater scatter, partly because the measurements are difficult, and partly because deviations from stoichiometry may effect it.) We have selected a high value of activation energy for lattice diffusion, Qυ, of the metal ion, for each oxide: 452 kJ/mole for UO2 and 625 kJ/mole for ThO2 (references are given in the table and the figures). This choice comes closest to agreement with creep data discussed below.
Grain-boundary diffusion of the metal ion has been measured in UO2. We have used the data of Alcock et al. (1966) [5] which are some three orders of magnitude slower than those of Yajima et al. (1966) [6] at 0.5 TM. When used in the diffusional creep equation, it comes closest to describing the creep observations of Poteat and Yust (1968) [7], predicting a creep rate about one order of magnitude slower than that observed.
In deriving power-law creep parameters, we have used the activation energy for lattice self-diffusion of the metal ion given in Table 13. 1 and chosen n and A to give the best fit to the power-law creep data. As Fig. 13.2 shows, our values for n and A for UO2 match the data of Poteat and Yust (1968) [7] at 1535°C, and give a tolerable fit to the rest of the high-stress data for stoichiometric UO2 from 1400 to 2000°C. Those for ThO2 (Fig. 13.4) match Wolfe and Kaufman's (1967) [8] data between 1700 and 1900°C, and are a tolerable fit to the high-stress data of Poteat and Yust (1966) [9].
At lower stresses and smaller grain-sizes, creep in UO2 becomes Newtonian-viscous (n = 1) and strongly dependent on grain size (Poteat and Yust, 1966, 1968 [7, 9]; Bohaboy et al., 1969 [10]; Seltzer et al., 1971 [1]; Burton and Reynolds, 1973 [11]). The data for both oxides are consistent with diffusional flow, usually involving grain-boundary transport, and sometimes with a threshold stress (Burton and Reynolds, 1973 [11]). An example is the study of the compressive creep of ThO2, with a grain size of 10 µm, of Poteat and Yust (1966) [9]. They observed an activation energy of 470 ± 30 kJ/mole, about three-quarters of that for lattice self-diffusion of Th ions. The absolute magnitude of the creep rate is faster, by a factor of 104, than that predicted by the Nabarro-Herring equation, but is broadly consistent with the Coble equation (Chapter 2, eqn. 2.29). We have adopted Qb = 0.6Qυ and δD0b = 10-14 m3/s, which adequately describes the diffusion measurements of King (1968) [12] for low-angle boundaries, and have used this in evaluating Coble-creep in ThO2, giving a tolerable match to the observed creep rates.
The creep data for both oxides were obtained from samples with grain sizes in the range 7 to 55 µm. Inspection of the figures, which are constructed for a grain size of 10 µm, suggests that the predicted position of the boundary between power-law creep and diffusional flow lies at stresses which are too low. It must be remembered that diffusion and creep in these oxides depends on stoichiometry and on purity, and because of this, a low activation energy for creep, like that observed by Poteat and Yust, may imply that diffusion is extrinsic.
Parameters describing the low-temperature plasticity of UO2 (Table 13.1) are based on yield strength measurements of Radford and Terwilliger (1975) [13] and room-temperature hardness and compressive strength measurements of Rice (1971) [14]. Those for ThO2 are based on the compressive strength data of Ryshkewitch (1941, 1942) [15, 16].
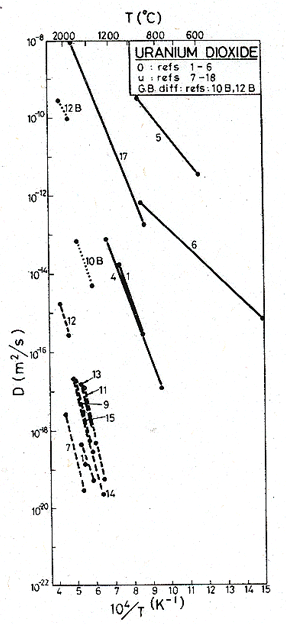
Fig. 13.5. Diffusion in UO2. The data are from (1) Dornelas adn Lacombe, 1967; (2) Contamin adn Stefani, 1967; (3) Contamin and Slodzian, 1968; (4) Marin and Contamin, 1969; (5) Lay, 1970; (6) Contamin et al., 1972; (7) Reinmann and Lundy, 1969; (8) ibid; 1968; (9) Auskern and Belle, 1961; (10) Alcock et al., 1966; (11)Lindner and Schmitz, 1961; (12) Yajima et al., 1966; (13) Hawkins and Alcock, 1968; (14)Nagels, 1966; (15) McNamara, 1963; (16) Carter and Lay, 1970; (17) Bittel et al., 1969; (18) Iida, 1967; (19) Matzke, 1969; (20) Murch et al., 1975.
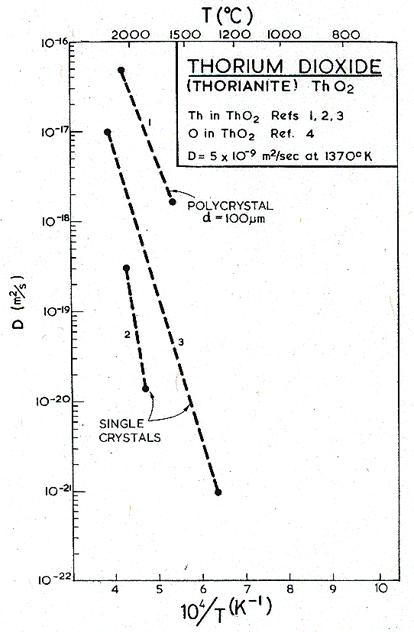
Fig. 13.6. Diffusion in ThO2. The data are from
(1) Kawkins and Alcock, 1968; (2) King, 1971; (3) Morgan and Poteat, 1968;
(4)
Roberts and Roberts, 1967