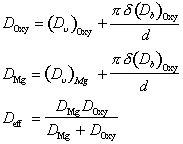CHAPTER 12

OXIDES WITH THE ROCK-SALT STRUCTURE:
MgO, CoO AND FeO

12.1 General Features of the Deformation of the Rock-Salt Structured Oxides

A number of simple oxides crystallize with the rocksalt structure; they include MgO, CaO, CdO, MnO, FeO, NiO, CoO, SrO and BaO. Some, like magnesia, are stable as the stoichiometric oxide MgO. Others, like cobalt monoxide, exist only as the hyperstoichiometric oxide Co_l–xO, always oxygen-rich because of the presence of Co³⁺ ions. Wustite, too, is always hyper-stoichiometric at atmospheric pressure, having the composition Fe_l–xO with 0.05 < x < 0.15. In all these oxides the oxygens are the larger ions. They are packed in an f.c.c. array, with the metal ions occupying the octahedral interstices.

Maps for MgO, CoO and FeO are shown in Figs. 12.1 to 12.10. The parameters used to construct them are listed in Table 12.1.

12.1 GENERAL FEATURES OF THE DEFORMATION OF THE ROCK-SALT STRUCTURED OXIDES

The bonding in rock-salt structured oxides is largely ionic. Like the alkali halides of Chapter 10, but unlike the transitional-metal carbides (Chapter 11), they slip easily on , though this provides only two independent slip systems. Polycrystal plasticity is made possible by slip on . But despite this similarity with the alkali halides, these oxides form a distinct isomechanical group: their melting points and moduli are much higher; their strength at 0 K is a little larger (about μ/30 compared with μ/50); and this low-temperature strength is retained to slightly higher homologous temperatures.

Above about 0.4 T_M the oxides start to creep. Once they do, their strength falls as fast or faster than that of the alkali halides. When creep of a compound is diffusion-controlled, both components—oxygen and metal in these oxides—must move. The creep rate is then controlled by a weighted mean of the diffusivities of the components. But diffusion may be intrinsic or extrinsic, and alternative diffusion paths (lattice and grain-boundary paths, for instance) may be available. As a general rule, the creep rate is determined by the fastest path of the slowest species—and this may change with temperature and grain size. The result is a proliferation of different diffusional flow fields—six or more are possible (Stocker and Ashby, 1973) [1].

This proliferation is illustrated below for magnesia. As the grain size decreases from 100 µm to 1 µm, new diffusional flow fields appear as new diffusion paths become rate-controlling. Even for this well-studied oxide the diffusion data are ambiguous and incomplete; we have had to guess values for some of the coefficients. But despite this, the picture is full enough to give a fair idea of how this, and the other oxides, should behave. All compounds, potentially, can show such complications; the figures for α-alumina (Chapter 14 and Section 14.1) give a further example. They are not shown on the other figures in this part of the book only because diffusion data are too meagre to allow them to be predicted with any precision.

A general review of the mechanical behavior of ceramics, including MgO, is given by Evans and Langdon (1976) [2]. It is recommended for further background.

12.2 DATA FOR MgO

The shear modulus and its temperature dependence were calculated from single-crystal data, using together with the measurements of Speltzler and Anderson (1971) [3] between 500 and 1000 K. The normalized temperature dependence (T_M/µ₀ · dµ/dT) is higher than that for other oxides; but it was calculated from the low-temperature data, where relaxation should be minimal.

The easy slip systems in MgO are those of the family <110> {110} (Parker, 1961) [4]. Slip on the harder family <011> {100} is observed in single crystals loaded along a <111> axis, and in polycrystals at high temperatures, and it is presumed to occur in test on polycrystals at low temperatures (Hulse and Pask, 1960 [5]; Hulse et al., 1963 [6]; Day and Stokes, 1966 [7]). It is this system which determines the low-temperature strength.

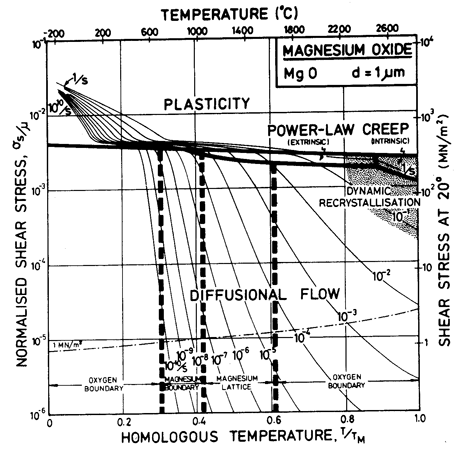
Fig.12.1. A stress/temperature map for MgO with a grain size of 1 µm. Data are shown on Fig. 12.3.

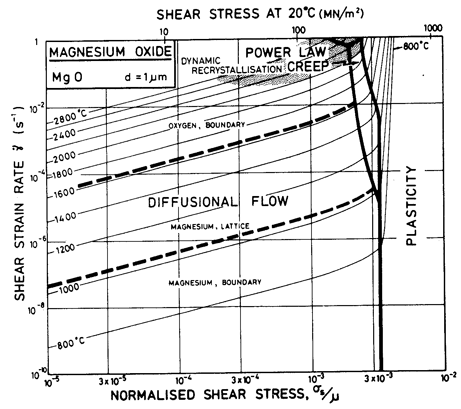
Fig.12.2. A strain-rate/stress map for MgO with a grain size of 1 µm. Data are shown on Fig. 12.4.

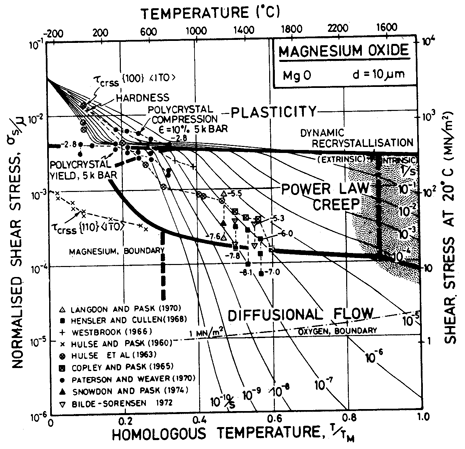
Fig.12.3. A stress/temperature map for MgO with a grain size of 10 µm. Data are labelled with log₁₀().

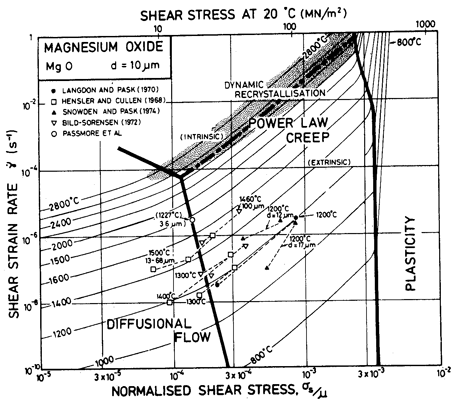
Fig.12.4. A strain-rate/stress map for MgO with a grain size of 10 µm. Data are labelled with the temperature °C.

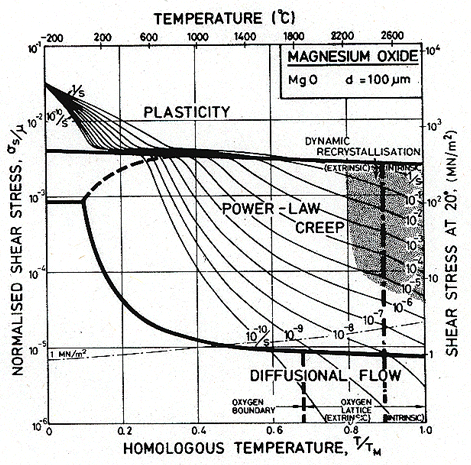
Fig.12.5. A stress/temperature map for MgO with a grain size of 100 µm. Data are shown on Fig. 12.3.

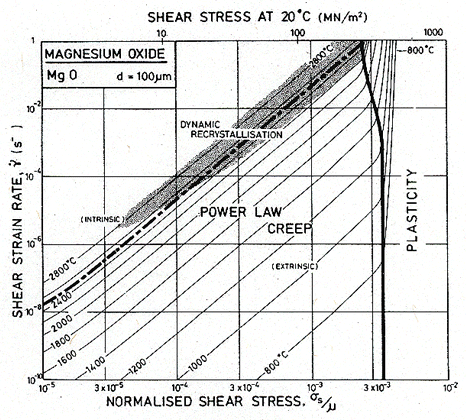
Fig.12.6. A strain-rate/stress map for MgO with a grain size of 100 µm. Data are shown on Fig. 12.4.

According to Wuensch et al. (1973) [8] lattice diffusion of Mg²⁺ in MgO is almost always extrinsic; accordingly, the extrinsic Mg²⁺ diffusion constants are based on their data. The rate of O^2- diffusion is much lower than that of Mg²⁺. We have attributed the O^2- diffusion rates measured by Oishi and Kingery (1960) [9] (who found Q_υ = 261 kJ/mole) to extrinsic diffusion, and those of Narayan and Washburn (1973) [10] (who found Q_υ = 460 kJ/mole) to intrinsic diffusion. Using the parameters listed in Table 12.1, O^2- diffusion becomes intrinsic above 0.9 T_M^. The maps show a dash-dot line at 0.9 T_M, separating the regime of extrinsic from that of intrinsic lattice diffusion of oxygen.

The activation energy for boundary diffusion of O^2- is taken as 230 kJ/mole, which matches the Coble-creep data of Passmore et al. (1966) [11]. The pre-exponential is derived from data given by McKenzie et al. (1971) [12]. The boundary diffusion parameters for Mg²⁺ are merely an educated guess. Core diffusion data for O^2- are from Narayan and Washburn's (1973) [10] observations of shrinking loops.

This set of diffusion parameters for MgO leads to the subdivision of the diffusional flow field into a number of subfields, the size of which varies with grain size. In general, the creep rate is controlled by the slower species moving on the fastest path available to it. When both Mg²⁺ and O^2- move by lattice diffusion, it is the oxygen which is slower, though even then the activation energy will change at the intrinsic to extrinsic transition. When boundaries offer a faster path for oxygen, the lattice diffusion of Mg²⁺ may become rate-controlling. Finally, if Mg²⁺ moves predominantly on boundaries, the boundary diffusion of oxygen becomes controlling.

This sequence, and the way it changes with grain size, are illustrated by Figs. 12.1 to 12.6. They were computed by using a new effective diffusion coefficient D_eff in place of eqn. (2.30), defined by:

Throughout, the faster of extrinsic diffusion and intrinsic was used. The rate-controlling species is best illustrated by a plot of D_υ and πδD_b/d for each species, against 1/T (Stocker and Ashby, 1973) [1]. Fig. 12.12 shows such a plot for two grain sizes: 1 µm and 100 µm. The size of the fields on the maps for these two grain sizes (Figs. 12.1 and 12.5) are determined by the intersection of the diffusion rates on Fig. 12.12, remembering that it is always the faster path of the slower species which is important.

The power-law creep parameters are based on the data of Langdon and Pask (1970) [13] at 1200°C, calculating A on the assumption that the creep rate at this temperature is limited by the extrinsic diffusion of oxygen. These parameters give a reasonable fit with other published data (see Figs. 12.3 and 12.4).

The low-temperature plasticity is based on the polycrystal yield data of Paterson and Weaver (1970) [14], who prevented fracture by applying a confining pressure of 500 MN/m². The results are consistent with the hardness data of Westbrook (1966) [15], and, as expected, are close to the shear stress required to operate the "hard" slip system , data for which are shown on Fig. 12.3.

12.3 DATA FOR Co_1–xO

Data for the moduli and other properties of CoO are complicated by its deviations from stoichiometry, and by the transition from anti-ferromagnetic to paramagnetic behavior at 289 K (Aleksandrov et al., 1968) [16]. Below this temperature, there is a slight tetragonal distortion of the structure, and the shear modulus decreases substantially.

We have neglected both, and calculated µ₀ (using ) from single-crystal constants at 300 K of Aleksandrov et al. (1968) [16]. Since its temperature dependence has not been measured with useful precision, we have adopted the "typical" value

Like magnesia, easy slip in CoO is found on the soft systems , with additional slip on the hard systems when compatibility requires it (CIauer et al., 1971a [17]; Krishnamachari and Jones, 1974 [18]).

As in MgO, oxygen is the slower diffusing species. Lattice diffusion of Co²⁺ in Co_1-xO depends on stoichiometry. The dominant defects are cobalt-ion vacancies, with a concentration x which decreases with decreasing oxygen partial pressure. Partly because of this, Co²⁺ diffuses at least 100 times faster than does O^2-, and with a much lower activation energy. From the data plotted in Fig. 12.13 we selected the oxygen diffusion data of Chen and Jackson (1969) [19] obtained under an oxygen partial pressure of 0.2 bars (one atmosphere of air); these conditions do not lead to stoichiometric CoO, but they are typical of much of the creep data. Boundary diffusion in CoO has not been measured directly; but creep data reviewed below suggest the values listed in the table. We have assumed an activation energy for core diffusion of Q_c = 0.6 Q_υ, giving a value of Q/RT_M very close to that measured for MgO.

The most extensive body of creep data for polycrystalline CoO is that of Krishnamachari and Notis (1977) [20]. They measured an activation energy of 301 kJ/mole, substantially lower than the preferred activation energy for oxygen diffusion (398 kJ/mole), and lower also than that measured in creep by Clauer et al. (1971a) [17] whose data, however, are for primary creep in single crystals. Using this higher activation energy, it is not possible to match Krishnamachari and Notis' data over a wide range of temperature. We have chosen creep parameters to give an exact match at 1100°C.

At low stress and high temperature, Krishnamachari and Notis (1977) [20] observed more or less Newtonian creep with an activation energy of 180 kJ/mole, suggesting Coble-creep. This is further supported by the observations of Clauer et al. (1971b) [21] and by Strafford and Gartside (1969) [22], of an activation energy of 213 kJ/mole during the lowstress creep of polycrystalline CoO. Considering these observations, we have chosen a value of Q_b of 200 kJ/mole (0.5 Q_υ) and a value of δD_0b which matches the Coble-creep equation (eqn. (2.29)) to the low-stress data of Krishnamachari and Notis (1977) [20]. Their data suggested a grain size dependence of 1/d² which they interpret as Nabarro-Herring, rather than Coble-creep. But lattice diffusion of oxygen is much too slow to account for the rates they observed, and if lattice diffusion of cobalt is rate-controlling, then boundary diffusion of oxygen must be even faster than we have assumed it to be (see the discussion for MgO). The unexpected grain size dependence may be caused by the proximity of the field boundary with dislocation creep.

Dislocation glide parameters are deduced from the hardness data of Westbrook (1966) [15], with the Marsh (1964) [23] correction.

The two maps (Figs. 12.7 and 12.8) are broadly consistent with the limited data. The real behavior may be complicated by transitions from intrinsic to extrinsic diffusion, and by oxygen transport by boundary diffusion while cobalt still moves by lattice diffusion. The effect of such changes is illustrated in the section on MgO.

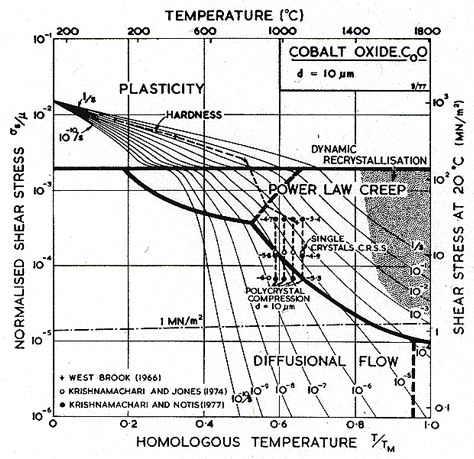
Fig.12.7. A stress/temperature map for CoO with a grain size of 10 µm. Data are labelled with log_l0().

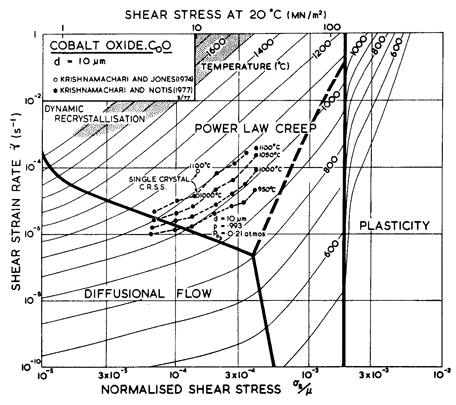
Fig. 12.8. A strain-rate/stress map for CoO with a grain size of 10 µm. Data are labelled with the temperature in °C.

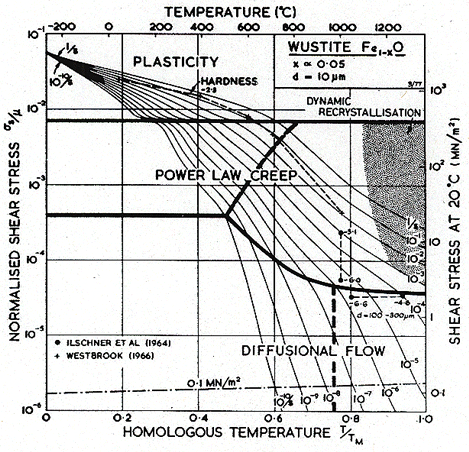
Fig.12.9. A stress/temperature map for FeO with a grain size of 10 µm. Data are labelled with log_l0().

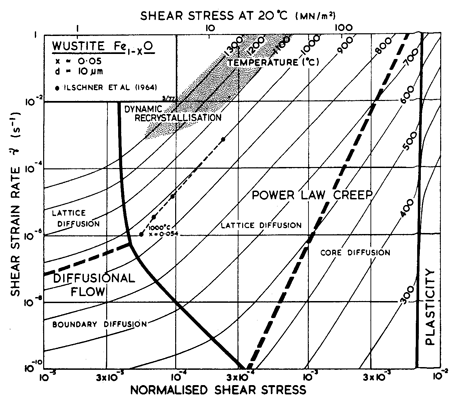
Fig.12.10. A strain-rate/stress map for FeO with a grain size of 10 µm. Data are labelled with the temperature in °C.

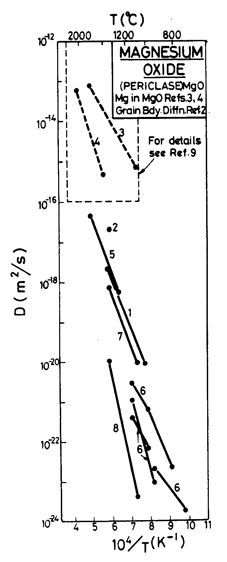
Fig. 12.11. Diffusion data plot for MgO. Data from (1) Shirasaki and Hama (1973) [24]; (2) Shirasaki and Oishi (1971) [25]; (3) Harding et al. (1971) [26]; (4) Vasilov et al. (1969); (5) Oishi and Kingery (1960); (6) Rovner (1966) [27]; (7) Shirasaki and Yamamura (1973); (8) Narayan and Washburn (1973) [10]; (9) Harding and Price (1972) [28].

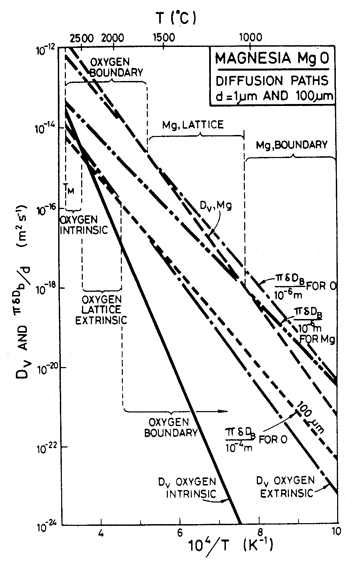
Fig. 12.12. Selected diffusion coefficients for MgO illustrating the selection of the slowest species diffusing by the fastest path.

12.4 DATA FOR Fe_l-xO

No single-crystal elastic constants are available for FeO. Table 12.1 lists the polycrystal shear modulus of Akimoto (1972) [29], and the typical temperature dependence of –0.3. By analogy with the other oxides of this chapter, slip in FeO is expected to occur on the easy system with slip on the hard system appearing in polycrystals.

As in Co_l–xO, deviations from stoichiometry influence the properties of Fe_l–xO. Its melting point, for example, depends on composition; we have used the value for x = 0.05. More important, diffusion rates depend on composition. As far as we know, lattice diffusion of O^2-in Fe_l–xO has not been measured. The oxide is always hyperstoichiometric, and the metal ion is smaller than the oxygen ion. For both reasons we expect that the diffusion of O^2- should be much slower than that of Fe²⁺, and should control creep rates. The creep data of Ilschner et al. (1964) [30] support this view: they observed an activation energy for creep of 326 kJ/ mole, compared with about 125 kJ/mole for the lattice diffusion of Fe²⁺. We have therefore assumed that Q_υ (O^2-) is 326 kJ/mole even though it leads to a normalized value, Q_υ/RT_M, of 24 which is higher than that for most other oxides. We have combined this with a pre-exponential D₀_υ (O^2-) of 10^-2 m²/s to give a melting point diffusivity in general agreement with that for other oxides. There are no measurements of grain-boundary or core diffusion for FeO. The data given in the table are estimates.

The parameters describing power-law creep are chosen to fit the data of Ilschner et al. (1964) [30] for x = 0.054. The creep rate of both Co_1–xO and Fe_l–xO increases with x, an observation not easy to explain if the creep is controlled by oxygen diffusion on its own sublattice. It is possible that complex oxygen defects are involved.

The parameters for lattice-resistance controlled glide are chosen to fit the hardness data of Westbrook (1966) [15], adjusted according to Marsh (1964) [23]. The simple maps of Figs. 12.9 and 12.10 are consistent with this very limited data. One must anticipate that the real behavior may be complicated in the ways described for MgO.

Fig. 12.13. Diffusion data plot for CoO. Data from (l) Maiya et al. (1970); (2) Mrowec (1967); (3) Chen et al. (1969); (4) Carter and Richardson (1954) [31]; (5) Crow (1969); (6) Chen and Jackson (1969); (7) Holt (1967); (8) Thompson (1962).

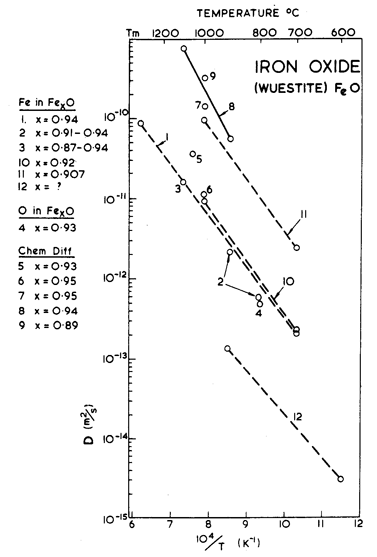
Fig. 12.14. Diffusion data plot for FeO. Data from (1) Chen and Peterson (1973) [32]; (2) Greenwood and Howe (1972) [33]; (3) and (4) Hembree and Wagner (1969) [34]; (5) Campbell (1969) [35]; (6) Fujii and Meussner (1967) [36]; (7) Levin and Wagner (1965) [37]; (8) Rickert and Weppner (1974) [38]; (9) Chu (1973) [39]; (10) Carter and Richardson (1954) [31]; (11) Himmel et al. (1953) [40]; (12) Valov (1970) [41].

References for Chapter 12

1. Stocker, R.L. and M.F. Ashby, On the empirical constants in the Dorn equation. Scripta Met., 1973. 7: p. 115-20.

2. Evans, A.G. and T.G. Langdon, Structural Ceramics. Prog. Mat. Sci., 1976. 21.

3. Speltzler, H.A. and D.L. Anderson, Discrepancies in elastic constant data for MgO polycrystals and single crystals. J. Am. Ceram. Soc., 1971. 54: p. 520-5.

4. Parker, E.R., Mechanical Properties of Engineering Ceramics, ed. W.W.a.P. Kriegel, H. 1961, Inter-science, NY. 61.

5. Hulse, C.O. and J.A. Pask, Mechanical properties of magnesia single crystals in compression. Journal of American Ceramic Society, 1960. 43: p. 373-84.

6. Hulse, C.O., S.M. Copley, and J.A. Pask, Effect of crystal orientation on plastic deformation of magnesium oxide. Journal of American Ceramic Society, 1963. 46: p. 317-322.

7. Day, R.B. and R.J. Stokes, Mechanical behavior of polycrystalline magnesium oxide at high temperatures. Journal of American Ceramic Society, 1966. 49: p. 345-54.

8. Wuensch, B.J., W.C. Steele, and T. Vasilos, cation self-diffusion in single-crystal MgO. J. Chem. Phys., 1973. 58: p. 5258-66.

9. Oishi, Y. and W.D. Kingery, J. Chem. Phys., 1960. 33: p. 905.

10. Narayan, J. and J. Washburn, Self diffusion in magnesium oxide. Acta Met., 1973. 21: p. 533.

11. Passmore, E.M., R.H. Duff, and T. Vasilov, Creep of dense, polycrystalline magnesium oxide. J. Am. Ceram. Soc., 1966. 49: p. 594-600.

12. McKenzie, D.P., The History of the Earth's Crust, ed. R.A. Phinney. 1968, Princeton, N.J: Princeton University Press.

13. Langdon, T.G. and J.A. Pask, The mechanism of creep in polycrystalline magnesium oxide. Acta Metallurgica (pre 1990), 1970. 18: p. 505.

14. Paterson, M.S. and C.W. Weaver, Deformation of polycrystalline MgO under pressure. J. Am. Ceram. Soc., 1970. 53: p. 463-71.

15. Westbrook, J.H., Rev. Hautes Temper. et Refract., 1966. 3: p. 47.

16. Aleksandrov, K.S., L.A. Shabanova, and L.M. Reshchikova, Anomalies of elastic properties and internal friction of a CoO single crystal. Sov. Phys. Solid State, 1968. 10: p. 1316-21.

17. Clauer, A.H., M.S. Seltzer, and B.A. Wilcox, Creep of CoO single crystals. Journal of Materials Science, 1971a. 4: p. 1379-88.

18. Krishnamachari, V. and J.T. Jones, Compressive creep of CoO single-crystals. Journal of American Ceramic Society, 1974. 57: p. 506-7.

19. Chen, W.K. and R.A. Jackson, Oxygen self-diffusion in undoped and doped cobaltous oxide. J. Phys. Chem. Solids, 1969. 30: p. 1309-14.

20. Krishnamachari, V. and M.R. Notis, High temperature deformation of polycrystalline NiO and CoO. Acta Metallurgica (pre 1990), 1977. 25: p. 1025.

21. Clauer, A.H., M.S. Seltzer, and B.A. Wilcox, in Ceramics in Severe Environments, W.W.a.P. Kriegel, H, Editor. 1971b, Plenum. p. 361.

22. Strafford, K.N. and H. Gartside, The creep of CoO scales- the influence of stoichiometry, stress and temperature. Journal of Materials Science, 1969. 4(9): p. 760-7.

23. Marsh, D.M. Plastic flow in glass. in Proc. R. Soc. 1964.

24. Shirasaki, S. and M. Hama, Oxygen-diffusion characteristics of loosely-sintered polycrystalline MgO. Chem. Phys. Lett., 1973. 20: p. 361-5.

25. Shirasaki, S. and Y. Oishi, Role of grain boundaries in oxygen self-diffusion in polycrystalline MgO. Jap. J. Appl. Phys., 1971. 10: p. 1109-10.

26. Harding, B.C., D.M. Price, and A.J. Mortlock, cation self-diffusion in single crystal MgO. Philosophical Magazine, 1971. 23(182): p. 399-408.

27. Rovner, L.H. 1966, Cornell University.

28. Harding, B.C. and D.M. Price, Cation self-diffusion in MgO up to 2350 degrees C. Philosophical Magazine, 1972. 26(26): p. 253-60.

29. Akimoto, S., The system MgO-FeO-SiO₂ at high temperatures: Phase equilibra and elastic properties. Tectonophysics, 1972. 13: p. 161-200.

30. Ilschner, B., B. Reppich, and E. Riecke, Faraday Soc. Disc., 1964. 38: p. 243.

31. Carter, R.E. and F.D. Richardson, An Examination of the decrease of surface-activity method of measuring self-diffusion coefficients in Wustite and Cobaltous oxide. Journal of Metals, 1954. 6: p. 1244-57.

32. Chen, W.K. and N.L. Peterson, J. Phys. (Paris), Colloq., 1973. 9: p. 303.

33. Greenwood, N.N. and A.T. Howe, J. Chem. Soc. Dalton Trans., l972. 1: p. 122.

34. Hembree, P. and J.B.J. Wagner, The diffusion of Fe₅₅ in Wustite as a function of composition at 1100^o C. Trans. AIME, 1969. 245: p. 1547.

35. Campbell, R.H. 1969, Arizona State University, p. 95. Univ. Microf. No. 69-5710.

36. Fujii, C.T. and R.A. Meussner, Rept. Nav. Res Lab. Progr. (no report #). 1967.

37. Levin, R.L. and J.B.J. Wagner, Reduction of undoped and chromium-doped wustite in carbon monoxide-carbon dioxide mixtures. Trans. AIME, 1965. 233: p. 159.

38. Rickert, H. and W. Weppner, Electrochemical investigation of chemical diffusion in wustite using a solid oxide electrolyte. Z. Naturforsch., 1974. A29: p. 1849-59.

39. Chu, W.F. in Proc. Nato Conf Sept. 1973. Belgirate, Italy.: North Holland Publ. Co.

40. Himmel, L., R.F. Mehl, and C.E. Birchenall, Self-diffusion of iron in iron oxides and Wagner theory of oxidation. J. Metals, 1953. 5: p. 827-43.

41. Valov, P.M., J. Solid State Chem., 1970. 1: p. 215.