CHAPTER  11

---

THE TRANSITION-METAL CARBIDES: ZrC AND TiC

 

11.1 General Features of the Mechanical Behaviour of Transition-Metal Carbides

11.2 Origins of Data for Transition-Metals Carbides

References for Chapter 11

 

ZIRCONIUM CARBIDE and titanium carbide typify a large group of refractory carbides with the rock-salt structure (examples are TiC, ZrC, HfC, VC, NbC, TaC). They form part of a larger group of over 80 hydrides, borides and carbides with this structure. They differ from alkali halides in that the bonding is less ionic in character: it is sometimes helpful to think of them as interstitial compounds based on metallic zirconium, titanium, etc. Almost all of them are very hard: they are used for cutting tools, abrasives and dies. Mechanical data are available for only a few; we consider TiC and ZrC as typical.

            Maps and data for ZrC are shown in Figs. 11.1 and 11.2. Those for TiC are so nearly identical that, although the data are discussed below, no additional maps are given. The parameters used to compute the maps are listed in Table 11.1.

 

TABLE 11.1 The transition-metal carbides

 

 

11.1 GENERAL FEATURES OF THE MECHANICAL BEHAVIOUR OF TRANSITION-METAL CARBIDES

<Back to Top>

 

            These carbides are characterized by large elastic moduli (μ₀ ≈ 200 GN/m²) and high melting tem­peratures (circa 3500 K). At low temperatures they are extremely hard, among the hardest known materials, with yield strengths which (at 0 K) approach the ideal strength (Fig. 11.1). Yet at high homologous temperatures they are very soft; or, more accurately, they creep exceptionally rapidly. This behaviour is related to two important proper­ties of these carbides: at low temperatures they have an exceptionally high lattice resistance to disloca­tion glide: but at high temperatures the diffusivity of the metal ions is exceptionally rapid.

            The primary glide system in single crystals is , with a Burger's vector of ; slip on {100} and {110} is also observed (Williams and Schaal, 1962 [1]; Hollox and Smallman, 1966 [2]; Lee and Haggerty, 1969 [3]). This implies (Williams, 1964 [4]) that there is little ionic contribution to the bonding, since charged ions would enforce  slip. Part, at least, of the bonding is metallic. The hard­ness of these materials falls rapidly between 0.2 and 0.4 T_M and at 0.5 T_M they are as soft, or softer, than pure copper at room temperature. (By contrast the high hardness of the diamond cubic elements Si and Ge, the covalent compounds SiC and Si₃N₄, and hydrogen-bonded ice, first starts to decrease at 0.5 T_M.) For this reason, the transition-metal carbides are not attractive as high-temperature materials: they creep rapidly at comparatively low temperatures. Dispersion strengthening by doping with borides to increase their creep strength remains a possibility.

 

 

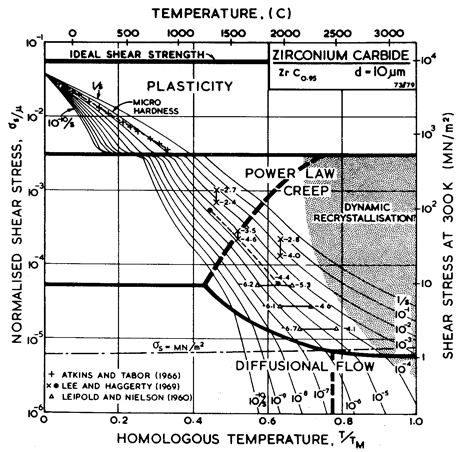
Fig. 11.1. A stress/temperature map for ZrC_0.95 of grain size 10 µm. Data are labelled with log₁₀().

 

 

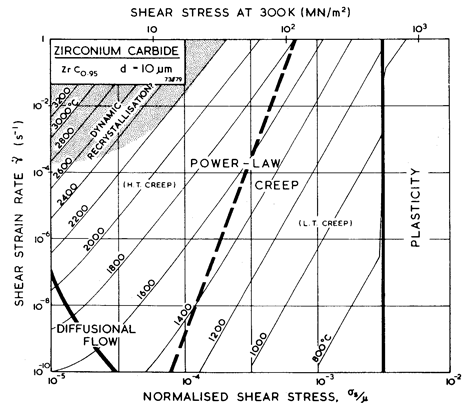
Fig. 11.2. A strain-rate/stress map for ZrC_0.9 of grain size 10 µm.

 

 

There is a considerable literature on the transition-metal carbides. The most important general references are: Atkins and Tabor (1966) [5] (hardness data); Lee and Haggerty (1969) [3] (slip and creep in ZrC); Hollox (1968) [6] and Hollox and Smallman (1966) [2] (slip and creep in TiC); Williams (1964) [4] (slip in single crystals of TiC); and the review by Williams (1971) [7]. Data from all these sources are included in Figs. 11.1, 11.2 and 11.3.

 

Fig. 11.3. Metal-ion and carbide diffusion in transition metal carbides. The diffusion coefficient has been normalized by the square of the Burger's vector. (l) Andrievskii et aL (1971) [8]; (2) Sarian (1968) [9]; (3) Villane (1968) [10]; (4) Brizes (1968) [11]; (5) Brizes et al. (1966) [12]; (6) Kohlstedt et al (1970) [13]; (7) Sarian (1969) [14]; (8) Andrievskii et al. (1969) [15]; (9) Bornstein et al. (1965) [16]; (10) Sarian and Criscione (1967) [17]; (11) Lidner et al (1967) [18].

 

 

11.2 ORIGINS OF DATA FOR TRANSITION-METAL CARBIDES

<Back to Top>

 

Much of the data used here for ZrC is from Lee and Haggerty (1969) [3] and refers to ZrC_0.945. Where possible, the TiC data refer to TiC_0.97. Moduli were calculated from single-crystal data using .

Figs. 11.1 and 11.2 show maps for ZrC_0.95 with a grain size of 10 µm. They are based on data shown on Fig. 11.1, and on data inferred from studies of TiC_0.97. The parameters used to compute the maps are listed in Table 11.1, together with relevant in­formation for TiC_0.97.

Diffusion data for carbides are plotted (on nor­malized axes) in Fig. 11.3. The metal ion diffuses much more slowly than does the carbon (typically, by a factor of 10^-3); it is metal-ion diffusion which will determine the rate of dislocation climb or of diffusional flow. Most of the transition metal car­bides exist in the hypostoichiometric (C-deficient) state. The carbon deficiency is taken up by vacancies on the carbon sub-lattice (which, under certain circumstances, may order). The transport of carbon then depends on composition; but as far as is known, diffusion of the metal ion is by a thermal­vacancy mechanism, and is independent of stoichio­metry (Sarian, 1968, 1969) [9, 14]. We have selected values for D_0υ and Q_υ for the metal ion which are consistent with the data plotted in Fig. 11.3, using data from Andrievskii et al. (1971) [8] for Zr and from Sarian (1968) [9] for Ti.

There are very little data for boundary and core diffusion. What little there is appears on Fig. 11.3. Data for UC (Villane, 1968) [10] and TiC (Hollox and Smallman, 1966) [2] suggest, respectively, that en­hanced boundary and core diffusion occur in the carbides. Our values (Table 11.1) are chosen to be consistent with these data and with observations of creep rates (see below).

Creep data for the transition metal carbides are limited to high temperatures (Keihn and Kebler, 1964 [19]; Hollox, 1968 [6]; Lee and Haggerty, 1969 [3]; and Liepold and Nielson,1964 [20]). Microstructural studies suggest a creep process very like that in pure metals: cells form, and (as far as one can judge from the meagre data) the activation energy is close to that of self-diffusion. Single crystals of ZrC show a well­developed power-law regime, with an exponent n of 5 (Lee and Haggerty, 1969) [3]. Polycrystals, too, show power-law creep and there is evidence of dif­fusional flow at low stresses (Liepold and Nielson, 1964) [20].

For TiC the creep data are more limited. Keihn and Kebler (1964) [19] give an activation energy of 732 kJ/mole for creep above 2000°C, and 544 kJ/mole below. This seems self-consistent, since 732 kJ/mole is almost exactly the activation energy for bulk diffusion of Ti. We have assumed n = 5 (the value observed for ZrC) and calculated the constant A from the best fit to their data. The detailed fitting process by which we make final adjustments to the parameters A and n (Chapter 3) has not been performed for TiC; the raw data are presented here for comparison with those for ZrC.

The lattice-resistance controlled glide parameters are based on microhardness measurements, extra­polated to 0 K, and on measurements of critical resolved shear strength. For both ZrC and TiC we used the microhardness data of Westbrook and Stover (1967), Atkins and Tabor (1966) [5] and Kornilov (1966) [21]. These data, treated as described in Chapter 3, using Marsh's (1964) [22] correction, com­bined with critical resolved shear stress measure­ments (Williams, 1964) [4] lead to values of  and ∆F_p given in Table 11.1.

 

 

References for Chatper 11

<Back to Top>

 

1.         Williams, W.S. and R.D. Schall, Elastic deformation, plastic flow, and dislocation in single crystals of titanium carbides. Journal of Applied Physics, 1962. 37: p. 955-62.

2.         Hollox, G.E. and R.E. Smallman, Plastic behaviour of titanium carbide. Journal of Applied Physics, 1966. 37: p. 818-23.

3.         Lee, D.W. and J.S. Haggerty, Plasticity and creep in single crystals of zirconium carbide. Journal of American Ceramic Society, 1969. 52: p. 641-7.

4.         Williams, W.S., Influence of temperature, strain rate, surface condition, and composition on the plasticity of transition-metal carbide crystals. Journal of Applied Physics, 1964. 35: p. 1329-38.

5.         Atkins, A.G. and D. Tabor, Hardness and deformation properties of solids at very high temperatures. Proceedings of the Royal Society of London, A., 1966. 292(1431): p. 441-59.

6.         Hollox, G.E., Microstructure and mechanical behavior of carbides. Mat. Sci. and Eng., 1968. 3: p. 121.

7.         Williams, W.S., Prog. Solid State Chem., 1971. 6: p. 57.

8.         Andrievskii, R.A., Y.F. Khormov, and I.S. Alekseeva, Self-diffusion of carbon and metal atoms in zirconium and niobium carbides. Fiz. Metal Metalloved, 1971. 32: p. 664-7.

9.         Sarian, S., Anomalous diffusion of ¹⁴C in TiC_0.67. Journal of Applied Physics, 1968. 39: p. 5O36-41.

10.       Villane, P., C.E.A. Report. 1968.

11.       Brizes, W.F., Journal of Nuclear Materials, 1968. 26: p. 227.

12.       Brizes, W.F., L.H. Cadoff, and L.M. Tobin, Journal of American Ceramic Society, 1966. 20: p. 57.

13.       Kohlstedt, D.L., W.S. Williams, and J.B. Woodhouse, Chemical diffusion in titanium carbide crystals. Journal of Applied Physics, 1970. 41: p. 4476-84.

14.       Sarian, S., Diffusion of ⁴⁴Ti in TiC_x. Journal of Applied Physics, 1969. 40: p. 3515-20.

15.       Andrievskii, R.A., V.V. Klimenko, and Y.F. Khormov, Self-diffusion of carbon in carbides of group IV and V transition metals. Fiz. Metal Metalloved, 1969. 28: p. 298-303.

16.       Bornstein, N.S., E.C. Hirakis, and L.A. Friedrich, Pratt and Whitney Report No. TIM-927. 1965, Pratt and Whitney.

17.       Sarian, S. and J.M. Criscione, Diffusion of carbon through zirconium monocarbide. Journal of Applied Physics, 1967. 38: p. 1794-98.

18.       Lidner, R., G. Riemer, and H.L. Scherff, Journal of Nuclear Materials, 1967. 23: p. 222.

19.       Keihn, F. and R. Kebler, J. Less Common Metals, 1964. 6: p. 484.

20.       Liepold, M.H. and T.H. Nielson, Mechanical properties of hot-pressed zirconium carbide tested to 2600^oC. Journal of American Ceramic Society, 1964. 47: p. 419-24.

21.       Kornilov, I.I., The Chemistry of Metallides,. 1966, Consultants Bureau, NY.

22.       Marsh, D.M. Plastic flow in glass. in Proc. R. Soc. 1964.