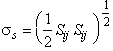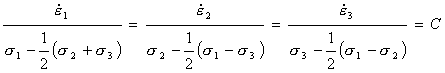The mechanisms may superimpose in complicated ways. Certain other mechanisms (such as superplastic flow) appear to be examples of such combinations.
Plastic flow of fully-dense solids is caused by the shearing, or deviatoric part of the stress field, σs. In terms of the principal stresses σ1, σ2 and σ3:
|
|
(1.1) |
or in terms of the stress tensor σij:
|
|
(1.2) |
| where |
|
(Very large hydrostatic pressures influence plastic flow by changing the material properties in the way described in Chapter 17, Section 17.4, but the flow is still driven by the shear stress σs.)
This
shear stress exerts forces on the defects—the dislocations, vacancies, etc.—in
the solid, causing them to move. The defects are the carriers of
deformation, much as an electron or an ion is a carrier of charge. Just as the
electric current depends on the density and velocity of the charge carriers,
the shear strain-rate,
![]() , reflects the density and velocity of
deformation carriers. In terms of the principal strain-rates
, reflects the density and velocity of
deformation carriers. In terms of the principal strain-rates
![]() ,
,
![]() and
and
![]() , this
shear
strain-rate is:
, this
shear
strain-rate is:
|
|
(l .3) |
or, in terms
of the strain-rate tensor
![]() :
:
|
|
(1.4) |
For simple
tension, σs and
![]() are
related to the tensile stress σ1 and
strain-rate
are
related to the tensile stress σ1 and
strain-rate ![]() by:
by:
|
|
(1.5) |
The
macroscopic variables of plastic deformation are the stress
σs, temperature T,
strain-rate
![]() and
the strain γ or
time t. If stress and temperature are prescribed (the independent variables), then the
consequent strain-rate and strain, typically, have the forms shown in Fig. l.la. At
low temperatures ( ~ 0.1 TM , where TM is
the melting point) the material work-hardens until the flow strength just
equals the applied stress. In doing so, its structure changes: the dislocation density (a microscopic, or
state variable) increases, obstructing further dislocation motion
and the strain-rate falls to zero, and the strain tends asymptotically to
a fixed value. If, instead, T and
and
the strain γ or
time t. If stress and temperature are prescribed (the independent variables), then the
consequent strain-rate and strain, typically, have the forms shown in Fig. l.la. At
low temperatures ( ~ 0.1 TM , where TM is
the melting point) the material work-hardens until the flow strength just
equals the applied stress. In doing so, its structure changes: the dislocation density (a microscopic, or
state variable) increases, obstructing further dislocation motion
and the strain-rate falls to zero, and the strain tends asymptotically to
a fixed value. If, instead, T and
![]() are
prescribed (Fig. 1.1b), the stress rises as the dislocation density rises.
But for a given set of values of this and the other state variables Si (dislocation
density and arrangement, cell size, grain size, precipitate size and spacing,
and so forth) the strength is determined by T and
are
prescribed (Fig. 1.1b), the stress rises as the dislocation density rises.
But for a given set of values of this and the other state variables Si (dislocation
density and arrangement, cell size, grain size, precipitate size and spacing,
and so forth) the strength is determined by T and
![]() ,
or (alternatively), the strain-rate is determined by
σs and
T.
,
or (alternatively), the strain-rate is determined by
σs and
T.
At higher temperatures (~ 0.5TM) , polycrystalline solids creep (Fig. 1.1, centre). After a transient during which the state variables change, a steady state may be reached in which the solid continues to deform with no further significant change in Si. Their values depend on the stress, temperature and strain-rate, and a relationship then exists between these three macroscopic variables.
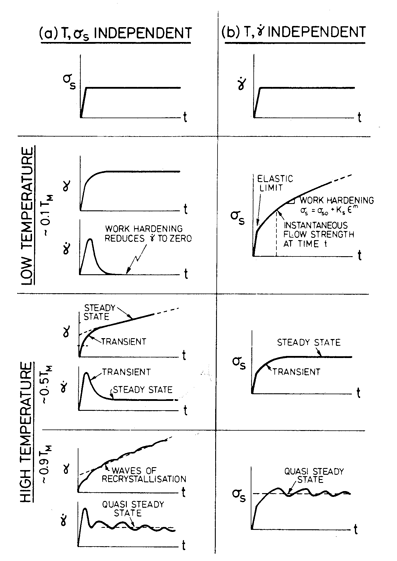
Fig. 1.1.
The way in which
σs ,T,
![]() and
γ are related for
materials (a) when
σs and T are prescribed and (b) when
and
γ are related for
materials (a) when
σs and T are prescribed and (b) when
![]() and T are
prescribed, for low temperatures (top), high temperatures (middle) and very
high temperatures (bottom).
and T are
prescribed, for low temperatures (top), high temperatures (middle) and very
high temperatures (bottom).
At very high temperatures (~ 0.9TM) the state variables, instead of tending to steady values, may oscillate (because of dynamic recrystallization, for instance: Fig. 1.1, bottom). Often, they oscillate about more or less steady values; then it is possible to define a quasi-steady state, and once more, stress, temperature and strain-rate are (approximately) related.
Obviously,
either stress or strain-rate can be treated as the independent variable.
In many engineering applications—pressure vessels, for instance—loads (and
thus stresses) are prescribed; in others—metal-working operations, for
example—it is the strain-rate which is given. To simplify the following
discussion, we shall choose the strain-rate
![]() as the independent
variable. Then each mechanism of deformation can be described by a rate
equation which relates
as the independent
variable. Then each mechanism of deformation can be described by a rate
equation which relates
![]() to the
stress σs, the temperature T,
and to the structure of the material at that instant:
to the
stress σs, the temperature T,
and to the structure of the material at that instant:
|
|
(1.6) |
As already stated, the set of i quantities Si are the state variables which describe the current microstructural state of the materials. The set of j quantities Pj are the material properties:: lattice parameter, atomic volume, bond energies, moduli, diffusion constants, etc.; these can be regarded as constant except when the plastic properties of different materials are to be compared (Chapter 18).
The state variables Si generally change as deformation progresses. A second set of equations describes their rate of change, one for each state variable:
|
|
(1.7) |
where t is time.
The individual components of strain-rate are recovered from eqn. (1.6) by using the associated flow rule:
|
|
(1.8) |
or, in terms of the stress and strain-rate tensors:
|
|
(1.9) |
where C is a constant.
The coupled set of equations (1.6) and (1.7) are the constitutive law for a mechanism. They can be integrated over time to give the strain after any loading history. But although we have satisfactory models for the rate-equation (eqn. (1.6)) we do not, at present, understand the evolution of structure with strain or time sufficiently well to formulate expressions for the others (those for dSi/dt). To proceed further, we must make simplifying assumptions about the structure.
Two alternative assumptions are used here. The first, and simplest, is the assumption of constant structure:
|
|
(1.10) |
Then the rate-equation
for
![]() completely
describes plasticity. The alternative assumption is that of steady state:
completely
describes plasticity. The alternative assumption is that of steady state:
|
|
(1.11) |
Then the
internal variables (dislocation density and arrangement, grain size, etc.) no
longer appear explicitly in the rate-equations because they are
determined by the external variables of stress and temperature. Using eqn.
(1.7) we can solve for S1, S2, etc., in terms of σs and T,
again obtaining an explicit rate-equation for
![]() .
.
Either simplification reduces the constitutive law to a single equation:
|
|
(1.12) |
since, for a given material, the properties Pj are constant and the state variables are either constant or determined by σs and T. In Chapter 2 we assemble constitutive laws, in the form of eqn. (1.12), for each of the mechanisms of deformation. At low temperatures a steady state is rarely achieved, so for the dislocation-glide mechanisms we have used a constant structure formulation: the equations describe flow at a given structure and state of workhardening. But at high temperatures, deforming materials quickly approach a steady state, and the equations we have used are appropriate for this steady behavior. Non-steady or transient behavior is discussed in Chapter 17, Section 17.1; and ways of normalizing the constitutive laws to include change in the material properties Pj are discussed in Chapter 18.
It
is useful to have a way of summarizing, for a given polycrystalline solid,
information about the range of dominance of each of the mechanisms of
plasticity, and the rates of flow they produce. One way of doing this (Ashby,
1972; Frost and Ashby, 1973; Frost, 1974) [1-3] is shown in Fig. 1.2. It
is a diagram with axes of normalized stress
σs/μ and
temperature, T/TM (where µ
is the shear modulus and TM the melting
temperature). It is divided into fields which show the regions of stress
and temperature over
which each of the deformation mechanisms is dominant. Superimposed on the
fields are contours of constant strain-rate: these show the net strain-rate
(due to an appropriate superposition of all the mechanisms) that a given
combination of stress and temperature will produce. The map displays the
relationship between the three macroscopic variables: stress as, temperature T and
strain-rate
![]() .
If any pair of these variables are specified, the map can be used to determine
the third.
.
If any pair of these variables are specified, the map can be used to determine
the third.
There are, of course, other ways of presenting the same information. One is shown in Fig. 1.3: the axes are shear strain-rate and (normalized) shear stress; the contours are those of temperature. Maps like these are particularly useful in fitting isothermal data to the rate-equations, but because they do not extend to 0 K they contain less information than the first kind of map.
A third type of map is obviously possible: one with axes of strain rate and temperature (or reciprocal temperature) with contours of constant stress (Figs. 1.4 and 1.5). We have used such plots as a way of fitting constant-stress data to the rate-equations of Chapter 2, and for examining behavior at very high strain-rates (Chapter 17, Section 17.2).

Fig. 1.2. A stress/temperature map for nominally pure nickel with a grain size of 0.1 mm. The equations and data used to construct it are described in Chapters 2 and 4.
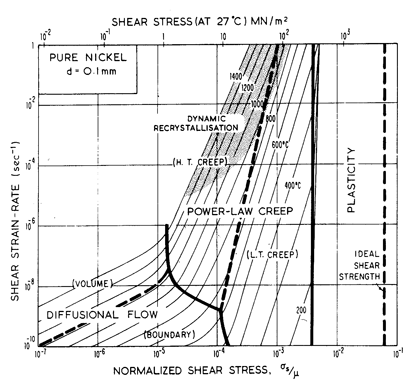
Fig. 1.3. A strain-rate/stress map for nominally pure nickel, using the same data as Fig. 1.2.
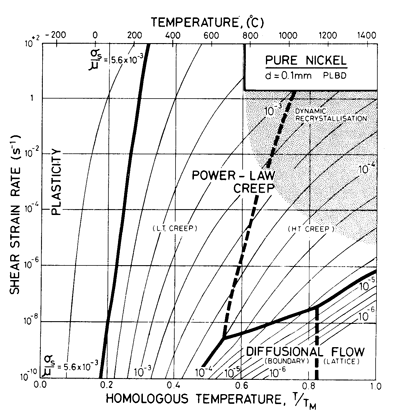
Fig. 1.4. A strain-rate/temperature map for nominally pure nickel, using the same data as Fig. 1.2.
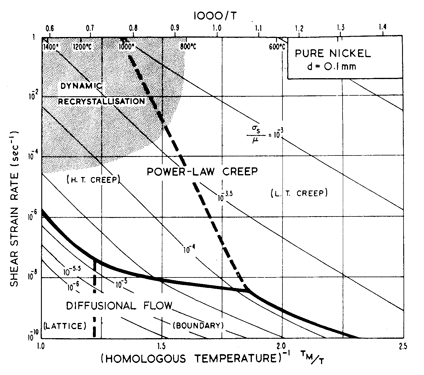
Fig. 1.5. A strain-rate/reciprocal temperature map for nominally pure nickel, using the same data as Fig. 1.2.
Finally, it is possible to present maps with a structure parameter (S1, S2, etc.) such as dislocation density or grain size as one of the axes (see, for example, Mohamed and Langdon, 1974) [4]. Occasionally this is useful, but in general it is best to avoid the use of such microscopic structure variables as axes of maps because they cannot be externally controlled or easily or accurately measured. It is usually better to construct maps either for given, fixed values of these parameters, or for values determined by the assumption of a steady state.
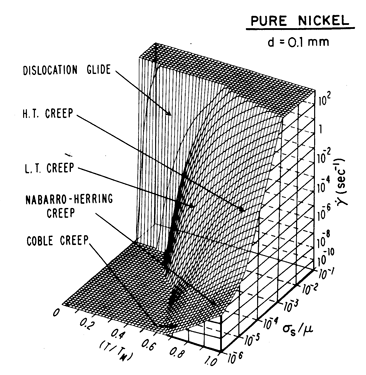
Fig. 1.6. A three-dimensional map for nominally pure nickel, using the same data as Figs. 1.2, 1.3 and 1.4.
Three of the maps shown above are orthogonal sections through the same three-dimensional space, shown in Fig. 1.6. In general, we have not found such figures useful, and throughout the rest of this book we restrict ourselves to two-dimensional maps of the kind shown in Figs. 1.2, 1.3 and, occasionally, 1.4.
One must be careful not to attribute too much precision to the diagrams. Although they are the best we can do at present, they are far from perfect or complete. Both the equations in the following sections, and the maps constructed from them, must be regarded as a first approximation only. The maps are no better (and no worse) than the equations and data used to construct them.